Complete the following multiplication table: Is the multiplication table symmetrical about the diagonal joining the upper left corner to the lower right corner?
To complete the multiplication table and determine if it is symmetrical about the diagonal, we will follow these steps:
Step 1: Set up the multiplication table
We will create a table with the numbers -4, -3, -2, -1, 0, 1, 2, 3, 4 along both the rows and columns.
Step 2: Fill in the table
Now we will fill in the table by multiplying the numbers from the rows and columns.
- Row for -4:
- -4 * -4 = 16
- -4 * -3 = 12
- -4 * -2 = 8
- -4 * -1 = 4
- -4 * 0 = 0
- -4 * 1 = -4
- -4 * 2 = -8
- -4 * 3 = -12
- -4 * 4 = -16
- Row for -3:
- -3 * -4 = 12
- -3 * -3 = 9
- -3 * -2 = 6
- -3 * -1 = 3
- -3 * 0 = 0
- -3 * 1 = -3
- -3 * 2 = -6
- -3 * 3 = -9
- -3 * 4 = -12
- Row for -2:
- -2 * -4 = 8
- -2 * -3 = 6
- -2 * -2 = 4
- -2 * -1 = 2
- -2 * 0 = 0
- -2 * 1 = -2
- -2 * 2 = -4
- -2 * 3 = -6
- -2 * 4 = -8
- Row for -1:
- -1 * -4 = 4
- -1 * -3 = 3
- -1 * -2 = 2
- -1 * -1 = 1
- -1 * 0 = 0
- -1 * 1 = -1
- -1 * 2 = -2
- -1 * 3 = -3
- -1 * 4 = -4
- Row for 0:
- 0 * -4 = 0
- 0 * -3 = 0
- 0 * -2 = 0
- 0 * -1 = 0
- 0 * 0 = 0
- 0 * 1 = 0
- 0 * 2 = 0
- 0 * 3 = 0
- 0 * 4 = 0
- Row for 1:
- 1 * -4 = -4
- 1 * -3 = -3
- 1 * -2 = -2
- 1 * -1 = -1
- 1 * 0 = 0
- 1 * 1 = 1
- 1 * 2 = 2
- 1 * 3 = 3
- 1 * 4 = 4
- Row for 2:
- 2 * -4 = -8
- 2 * -3 = -6
- 2 * -2 = -4
- 2 * -1 = -2
- 2 * 0 = 0
- 2 * 1 = 2
- 2 * 2 = 4
- 2 * 3 = 6
- 2 * 4 = 8
- Row for 3:
- 3 * -4 = -12
- 3 * -3 = -9
- 3 * -2 = -6
- 3 * -1 = -3
- 3 * 0 = 0
- 3 * 1 = 3
- 3 * 2 = 6
- 3 * 3 = 9
- 3 * 4 = 12
- Row for 4:
- 4 * -4 = -16
- 4 * -3 = -12
- 4 * -2 = -8
- 4 * -1 = -4
- 4 * 0 = 0
- 4 * 1 = 4
- 4 * 2 = 8
- 4 * 3 = 12
- 4 * 4 = 16
Step 3: Check for symmetry
To check for symmetry, we need to see if the values across the diagonal (from the top left to the bottom right) are the same.
- The diagonal values are:
- (1,1): 16
- (2,2): 9
- (3,3): 4
- (4,4): 1
- (5,5): 0
- (6,6): 1
- (7,7): 4
- (8,8): 9
- (9,9): 16
Now we compare:
- (1,2) with (2,1): 12 with 12
- (1,3) with (3,1): 8 with 8
- (1,4) with (4,1): 4 with 4
- (1,5) with (5,1): 0 with 0
- (1,6) with (6,1): -4 with -4
- (1,7) with (7,1): -8 with -8
- (1,8) with (8,1): -12 with -12
- (1,9) with (9,1): -16 with -16
Since all corresponding values are equal, the multiplication table is symmetric about the diagonal.
Conclusion
Yes, the multiplication table is symmetric about the diagonal joining the upper left corner to the lower right corner.
---
We will create a table with the numbers -4, -3, -2, -1, 0, 1, 2, 3, 4 along both the rows and columns.
Now we will fill in the table by multiplying the numbers from the rows and columns.
- -4 * -4 = 16
- -4 * -3 = 12
- -4 * -2 = 8
- -4 * -1 = 4
- -4 * 0 = 0
- -4 * 1 = -4
- -4 * 2 = -8
- -4 * 3 = -12
- -4 * 4 = -16
- -3 * -4 = 12
- -3 * -3 = 9
- -3 * -2 = 6
- -3 * -1 = 3
- -3 * 0 = 0
- -3 * 1 = -3
- -3 * 2 = -6
- -3 * 3 = -9
- -3 * 4 = -12
- -2 * -4 = 8
- -2 * -3 = 6
- -2 * -2 = 4
- -2 * -1 = 2
- -2 * 0 = 0
- -2 * 1 = -2
- -2 * 2 = -4
- -2 * 3 = -6
- -2 * 4 = -8
- -1 * -4 = 4
- -1 * -3 = 3
- -1 * -2 = 2
- -1 * -1 = 1
- -1 * 0 = 0
- -1 * 1 = -1
- -1 * 2 = -2
- -1 * 3 = -3
- -1 * 4 = -4
- 0 * -4 = 0
- 0 * -3 = 0
- 0 * -2 = 0
- 0 * -1 = 0
- 0 * 0 = 0
- 0 * 1 = 0
- 0 * 2 = 0
- 0 * 3 = 0
- 0 * 4 = 0
- 1 * -4 = -4
- 1 * -3 = -3
- 1 * -2 = -2
- 1 * -1 = -1
- 1 * 0 = 0
- 1 * 1 = 1
- 1 * 2 = 2
- 1 * 3 = 3
- 1 * 4 = 4
- 2 * -4 = -8
- 2 * -3 = -6
- 2 * -2 = -4
- 2 * -1 = -2
- 2 * 0 = 0
- 2 * 1 = 2
- 2 * 2 = 4
- 2 * 3 = 6
- 2 * 4 = 8
- 3 * -4 = -12
- 3 * -3 = -9
- 3 * -2 = -6
- 3 * -1 = -3
- 3 * 0 = 0
- 3 * 1 = 3
- 3 * 2 = 6
- 3 * 3 = 9
- 3 * 4 = 12
- 4 * -4 = -16
- 4 * -3 = -12
- 4 * -2 = -8
- 4 * -1 = -4
- 4 * 0 = 0
- 4 * 1 = 4
- 4 * 2 = 8
- 4 * 3 = 12
- 4 * 4 = 16
To check for symmetry, we need to see if the values across the diagonal (from the top left to the bottom right) are the same.
- (1,1): 16
- (2,2): 9
- (3,3): 4
- (4,4): 1
- (5,5): 0
- (6,6): 1
- (7,7): 4
- (8,8): 9
- (9,9): 16
- (1,2) with (2,1): 12 with 12
- (1,3) with (3,1): 8 with 8
- (1,4) with (4,1): 4 with 4
- (1,5) with (5,1): 0 with 0
- (1,6) with (6,1): -4 with -4
- (1,7) with (7,1): -8 with -8
- (1,8) with (8,1): -12 with -12
- (1,9) with (9,1): -16 with -16
Yes, the multiplication table is symmetric about the diagonal joining the upper left corner to the lower right corner.
Topper's Solved these Questions
Similar Questions
Complete the following table
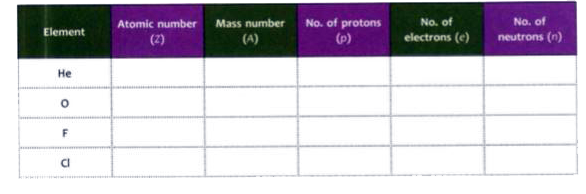 View Solution
View SolutionComplete the following table
 View Solution
View SolutionComplete the following table.
 View Solution
View SolutionComplete the following table .
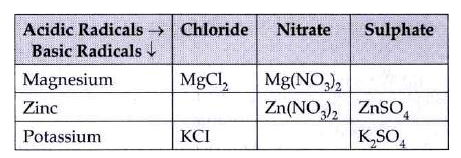 View Solution
View SolutionComplete the following table .
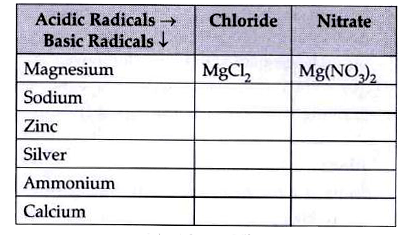 View Solution
View SolutionComplete the following table:
 View Solution
View SolutionComplete the following table :
 View Solution
View SolutionComplete the following table :
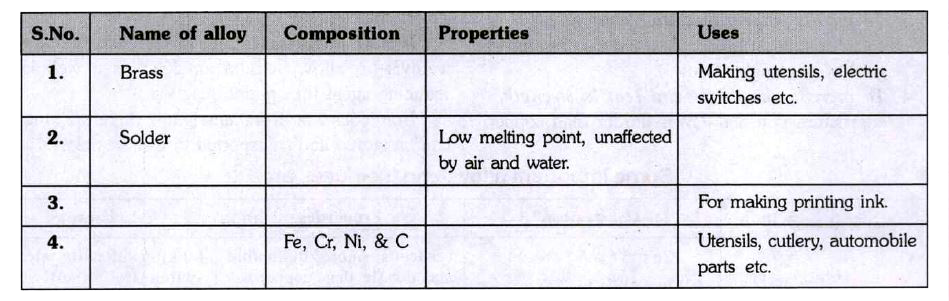 View Solution
View SolutionComplete the following table :
 View Solution
View SolutionComplete the following table.
 View Solution
View Solution

