Complex numbers z1 and z2 satisfy |z1|=2 and |z2|=3. If the included angle of their corresponding vectors is 60∘, then the value of 19∣∣∣z1−z2z1+z2∣∣∣2 is
5
6
7
8
The correct Answer is:C
(c) 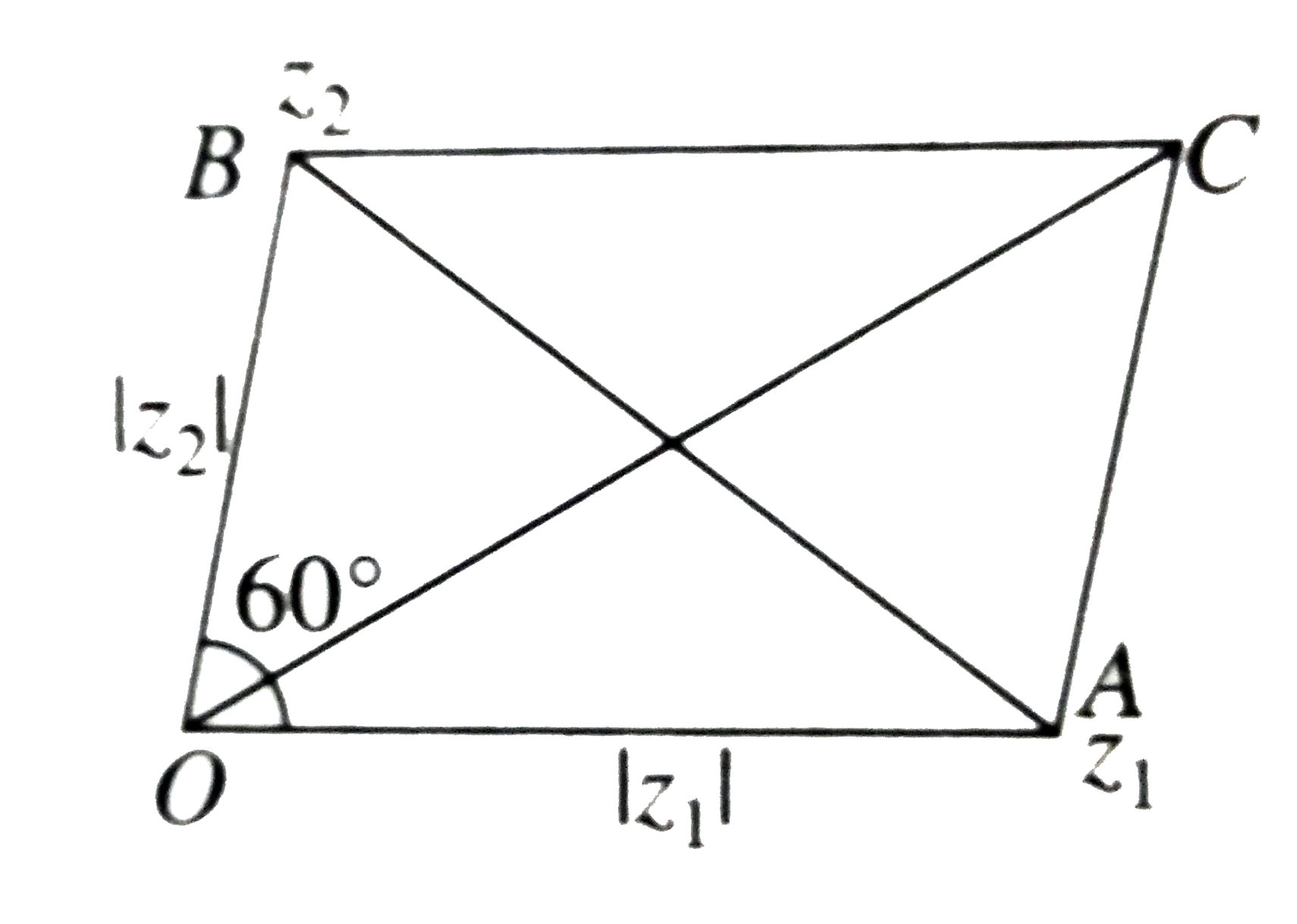
OC=|z1+z2| and AB=|z1−z2|
|z1+z2|=√|z1|2+|z2|2−2|z1||z2|cos120∘
=√4+9+2.3=√19
and |z1−z2|=√|z1|2+|z2|2−2|z1||z2|cos60∘
=√4+9−6=√7
∴∣∣∣z1−z2z1+z2∣∣∣=√719
∴19∣∣∣z1−z2z1+z2∣∣∣2=7
Topper's Solved these Questions
- COMPLEX NUMBERSBook:CENGAGEChapter:COMPLEX NUMBERSExercise:Matching Column
Explore 1 Video
- COMPLEX NUMBERSBook:CENGAGEChapter:COMPLEX NUMBERSExercise:Comprehension
Explore 11 Videos
- COMPLEX NUMBERSBook:CENGAGEChapter:COMPLEX NUMBERSExercise:Question Bank
Explore 30 Videos
- CIRCLESBook:CENGAGEChapter:CIRCLESExercise:Question Bank
Explore 32 Videos
- CONIC SECTIONSBook:CENGAGEChapter:CONIC SECTIONSExercise:Solved Examples And Exercises
Explore 91 Videos
Similar Questions
It is given the complex numbers z1 and z2, |z1|=2 and |z2|=3. If the included angle of their corresponding vectors is 60∘ , then find value of ∣∣∣z1+z2z1−z2∣∣∣
View SolutionIt is given that complex numbers z1 and z2 satisfy |z1|=2 and |z2|=3. If the included angle.of their corresponding vectors is 60∘ then ∣∣∣z1+z2z1−z2∣∣∣ can be expressed on √N7 where N is natural number then N equals
View Solution
Knowledge Check
It is given that complex numbers z1 and z2 satisfy |z1| =2 and |z2| =3 . If the included angle of their corresponding vectors is 60∘ , then ∣∣∣z1+z2z1−z2∣∣∣ can be expressed as √n√7 , where 'n' is a natural number then n=
A126B119C133D19For all complex numbers z1,z2 satisfying |z1|=12 and |z2−3−4i|=5, find the minimum value of |z1−z2|
A0B2C7D17For any two complex numbers z1,z2 the values of |z1+z2|2+|z1−z2|2, is
A|z1|2+|z2|2B2(|z1|2+|z2|2)C(|z1|+|z2|)2Dnone of these
It is given that complex numbers z1andz2satiy|z1|2and|z2|=3. If the included angled of their corresponding vectors is 600 , then find the value of ∣∣∣z1+z2z1−z2∣∣∣ .
View SolutionItis given that complex numbers z1 and z2 satisfy |z1|=2 and |z2|=3 If the included angle is 60∘ then z1+z2z1−z2 can be expressed as √N7 where N=
View SolutionFor all complex numbers z1,z2 satisfying |z1|=12and|z2−3−4i|=5, the minimum value of |z1−z2| is
View SolutionFor all complex numbers z1,z2 satisfying |z1|=12 and |z2−3−4i|=5, find the minimum value of |z1−z2|
View SolutionFor all complex number z1,z2 satisfying |z1|=12 and |z2−3−4ι|=5,then |z2−ιz1|
View Solution
