Complex numbers are the vertices A,B,C respectivelt of an isosceles right angled triangle with right angle at C. show that Solution in Bengali
Applying rotation about point B,
Applying rotation about point A,
Multiplying (1) and (2), we get
Topper's Solved these Questions
- COMPLEX NUMBERSBOOK - CENGAGE PUBLICATIONCHAPTER - COMPLEX NUMBERSEXERCISE - SLOVED EXAMPLES
15 Videos
- COMPLEX NUMBERSBOOK - CENGAGE PUBLICATIONCHAPTER - COMPLEX NUMBERSEXERCISE - EXERCISE3.1
4 Videos
- COMPLEX NUMBERSBOOK - CENGAGE PUBLICATIONCHAPTER - COMPLEX NUMBERSEXERCISE - Comprehension
11 Videos
- CIRCLESBOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLESEXERCISE - Comprehension Type
8 Videos
- CONIC SECTIONSBOOK - CENGAGE PUBLICATIONCHAPTER - CONIC SECTIONSEXERCISE - All Questions
102 Videos
Similar Questions
ifωandω2 are the nonreal cube roots of unity and [1/(a+ω)]+[1/(b+ω)]+[1/(c+ω)]=2ω2 and [1/(a+ω)2]+[1/(b+ω)2]+[1/(c+ω)2]=2ω , then find the value of [1/(a+1)]+[1/(b+1)]+[1/(c+1)].
View SolutionIs the following computation correct? If not give the correct computation: [√(−2).√(−3)]=√(−2).−3=√6
View SolutionConsider the region R in the Argand plane described by the complex number. Z satisfying the inequalities |Z−2|≤|Z−4|, |Z−3|≤|Z+3|, |Z−i|≤|Z−3i|, |Z+i|≤|Z+3i|
Answer the followin questions :
Maximum of |Z1−Z2| given that Z1, Z2 are any two complex numbers lying in the region R is
View Solution
In the diagram as shown, a circle is drawn with centre C(1,1) and radius 1 and a line L. The line L is tangent to the circle at Q. Further L meets the y-axis at R and the x-axis at P in such a way that the angle OPQ equals θ where 0<θ<π2.
Coordinate of Q is
View SolutionGiven that A(1,1) and B(2,−3) are two points and D is a point on AB produced such that AD=3AB. Find the coordinates of D.
View SolutionIf z_(1),z_(2),z_(3) are the vertices of an isosceles triangle right angled at z_(2), then prove that (z_(1))^(2)+2(z_(2))^(2)+(z_(3))^(2)=
View SolutionComplex numbers z_(1),z_(2),z_(3) are the vertices A,B,C respectively of an isosceles right angled trianglewith right angle at C and (z_(1)-z_(2))^(2)=k(z_(1)-z_(3))(z_(3)-z_(2)) then find k.
View SolutionComplex numbers of z1,z2,z3 are the vertices A, B, C respectively, of on isosceles right-angled triangle with right angle at C. show that (z1−z2)2 = 2(z1−z3)(z3−z2)
View SolutionComplex numbers z1,z2andz3 are the vertices A,B,C respectivelt of an isosceles right angled triangle with right angle at C. show that (z1−z2)2=2(z1−z3)(z3−z2).
View SolutionComplex numbers z1,z2,z3 are the vertices of A,B,C respectively of an equilteral triangle. Show that z21+z22+z23=z1z2+z2z3+z3z1.
View Solutionसमद्विबाहु समकोणीय त्रिभुज (C पर समकोण) से शीर्षो A,B,C द्वारा क्रमशः सम्मिश्र संख्याएँ z1,z2,z3 निरूपित है सिद्ध कीजिए कि
(z1−z2)2=2(z1−z3)(z3−z2)
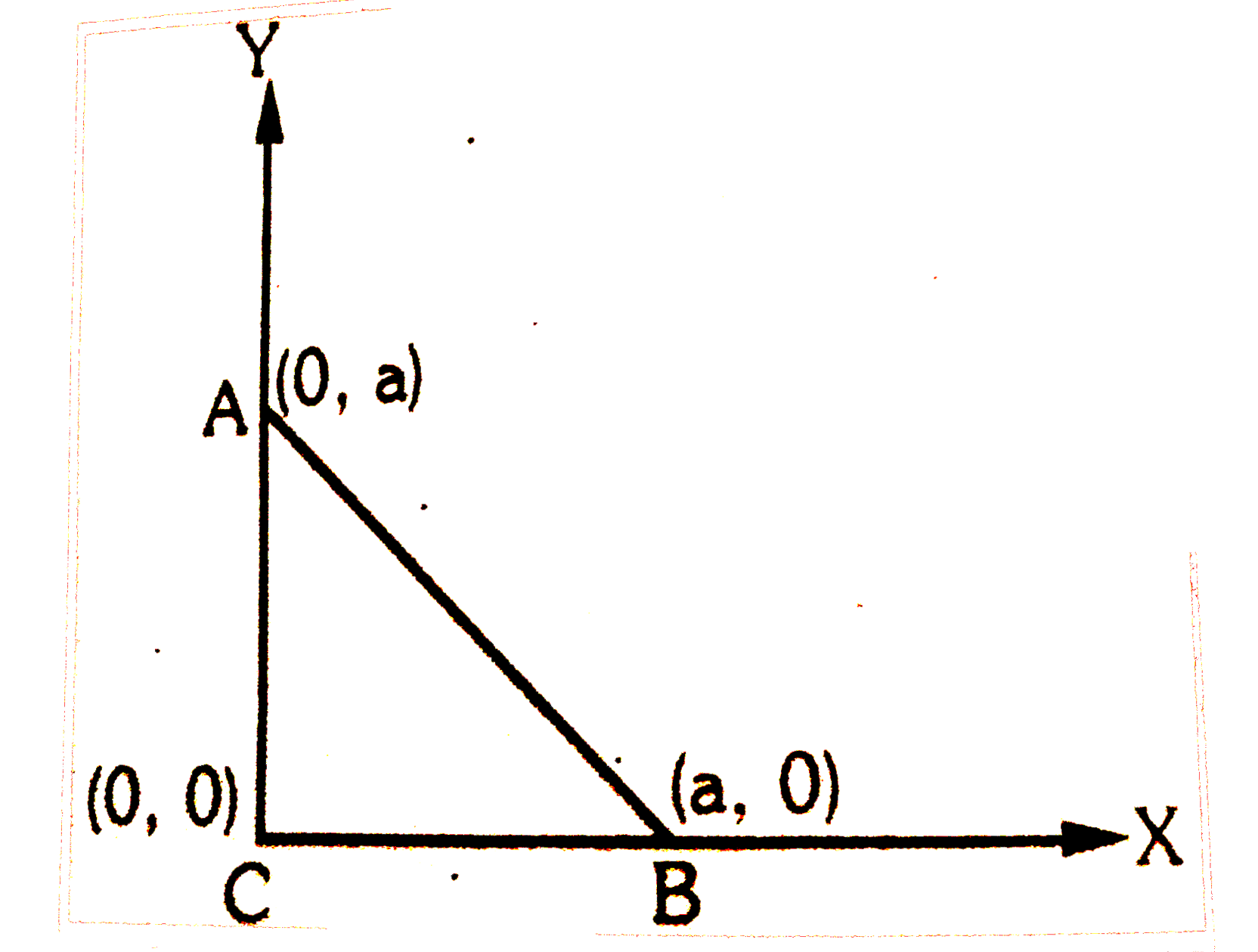
View SolutionThe vertices A,B,C of an isosceles right angled triangle with right angle at C are represented by the complex numbers z1z2andz3 respectively. Show that (z1−z2)2=2(z1−z3)(z3−z2).
View SolutionLet the complex numbers Z1,Z2andZ3 are the vertices A, B and C respectively of an isosceles right - angled triangle ABC with right angle at C, then the value of (Z1−Z2)2(Z1−Z3)(Z3−Z2) is equal to
View SolutionIf the complex numbers z1,z2 and z3 denote the vertices of an isoceles triangle, right angled at z1, then (z1−z2)2+(z1−z3)2 is equal to
View Solutionसम्मिश्र संख्यायें z1,z2,z3 क्रमशः समद्विबाहु समकोण त्रिभुज जो कि c पर समकोण है के शीर्ष A,B,C है तो प्रदर्शित कीजिए (z1−z2)2=2(z1−z3)(z3−z2)
View SolutionComplex numbers z1,z2andz3 are the vertices A,B,C respectivelt of an isosceles right angled triangle with right angle at C. show that (z1−z2)2=2(z1−z3)(z3−z2).
View Solution
