Concavity and convexity :
if f''(x)>0∀x∈(a,b) then the curve y=f(x) is concave up ( or convex down) in (a,b) and iff''(x)<0∀x∈(a,b) then the curve y=f(x) is concave down (or convex up ) in (a,b)
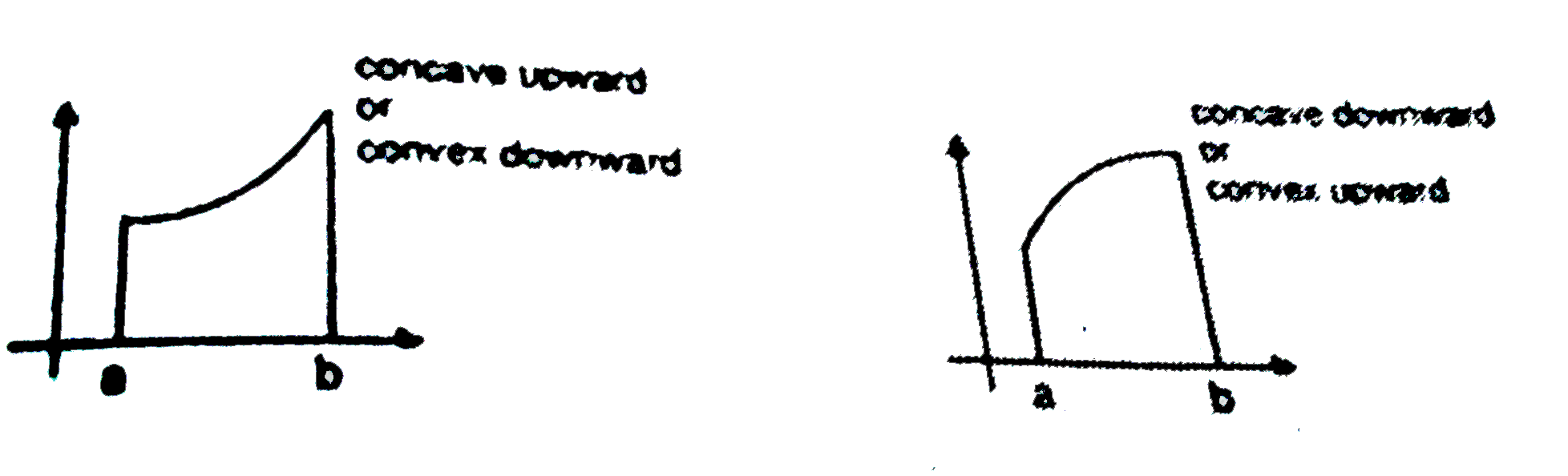
Inflection point :
The point where concavity of the curve changes is known as point of inflection (at inflection point f''(x) is equal to 0 or undefined)

Exhaustive set of values of 'a' for which the function f(x)=x4+ax3+3x22+1 will be concave upward along the entire real line is :
[−1,1]
[−2,2]
[0,2]
[0,4]
The correct Answer is:B
Step by step video, text & image solution for Concavity and convexity : if f''(x) gt 0 AA x in (a,b) then the curve y=f(x) is concave up ( or convex down) in (a,b) and if f''(x) lt 0 AA x in (a,b) then the curve y=f(x) is concave down (or convex up ) in (a,b) Inflection point : The point where concavity of the curve changes is known as point of inflection (at inflection point f''(x) is equal to 0 or undefined) Exhaustive set of values of 'a' for which the function f(x) =x^(4) +ax^(3)+(3x^(2))/(2)+1 will be concave upward along the entire real line is : by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- APPLICATION OF DERIVATIVESBOOK - RESONANCECHAPTER - APPLICATION OF DERIVATIVESEXERCISE - Exersise-3 Part I
27 Videos
- APPLICATION OF DERIVATIVESBOOK - RESONANCECHAPTER - APPLICATION OF DERIVATIVESEXERCISE - Exersise-3 Part II
22 Videos
- APPLICATION OF DERIVATIVESBOOK - RESONANCECHAPTER - APPLICATION OF DERIVATIVESEXERCISE - Exersise-2 Part III
23 Videos
- COMBINATORICSBOOK - RESONANCECHAPTER - COMBINATORICSEXERCISE - Exercise-2 (Part-II: Previously Asked Question of RMO)
8 Videos
Similar Questions
Knowledge Check
Concavity and convexity :
if f''(x)>0∀x∈(a,b) then the curve y=f(x) is concave up ( or convex down) in (a,b) and iff''(x)<0∀x∈(a,b) then the curve y=f(x) is concave down (or convex up ) in (a,b)

Inflection point :
The point where concavity of the curve changes is known as point of inflection (at inflection point f''(x) is equal to 0 or undefined)
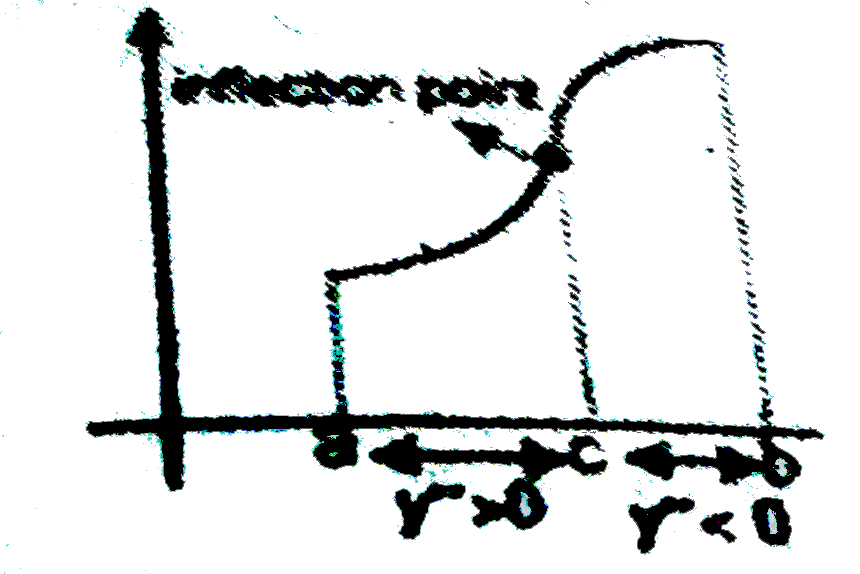
Number of point of inflection for f(x)=(x−1)3(x−2)2 is :A1B2C3D4Let g'(x)>0andf'(x)<0∀x∈R, then
Ag(f(x+1))>g(f(x−1))Bf(g(x−1))<f(g(x+1))Cg(f(x+1))<g(f(x−1))Dg(g'(x+1))<g(g(x+1))If f''(x)>0∀x∈R,f'(4)=0 and g(x)=f(cot2x−2cotx+5),0<x<π2 , then
Ag(x) is increasing in (0,π2)Bg(x) is decreasing in (0,π2)Cg(x) is increasing in (π4,π2)Dg(x) is decreasing in (0,π4)
b.Concave lens and Convex Lens.
View SolutionThe length of curve: y=f(x) between x=a and x=b is given by
View SolutionLet (a,b) and (λ,u) be two points on the curve y=f(x). If the slope of the tangent to the curve at (x,y) be ?
View SolutionLet f(x) be a continuous function, ∀x∈R,f(0)=1andf(x)≠x for any x∈R, then show f(f(x))>x,∀x∈R+
View SolutionIf f'(x)=x−1, the equation of a curve y=f(x) passing through the point (1, 0) is given by
View Solution
