Consider equation ((x2+x)2)+a(x2+x)+4=0 Match the values of a in Lits II for the types of roods in Lits I. Solution in Bengali
abcd(1)pqrs
abcd(2)qrrp
abcd(3)rpsq
abcd(4)qspr
The correct Answer is:1
(x2+x)2+a(x2+x)+4=0
Let t=x2+x=(x+1/2)2−1/4.
⇒t∈[−14,∞]
Now, f(t)=t2+at+4=0 ....(1)
(a) All four real and distinct roots.
So, equation (1) has both roots greater then −1/4.

Following conditions are required:
(i)D>0⇒a2−16>0⇒|a|>4
(ii) f(−1/4)=116−a4+4>0⇒a<65/4
(iii) −B2A=a2>−14⇒a<12
⇒a∈(−∞,−4)
(b) Two real roots which are distinct.

⇒f(−1/4)<0
⇒a>65/4
⇒a∈(65/4,∞)
(c) All four roots are imaginary.

(i) D≥0⇒|a|≥4
(ii) f(−1/4)>0⇒a<654
(iii) −B2A<−14⇒a>12⇒a∈[4,654]
Case II:
D<0
⇒a∈(−4,4) ....(2)
From case I and case II,
a∈(−4,654)
(d) Four real roots in which two are equal.
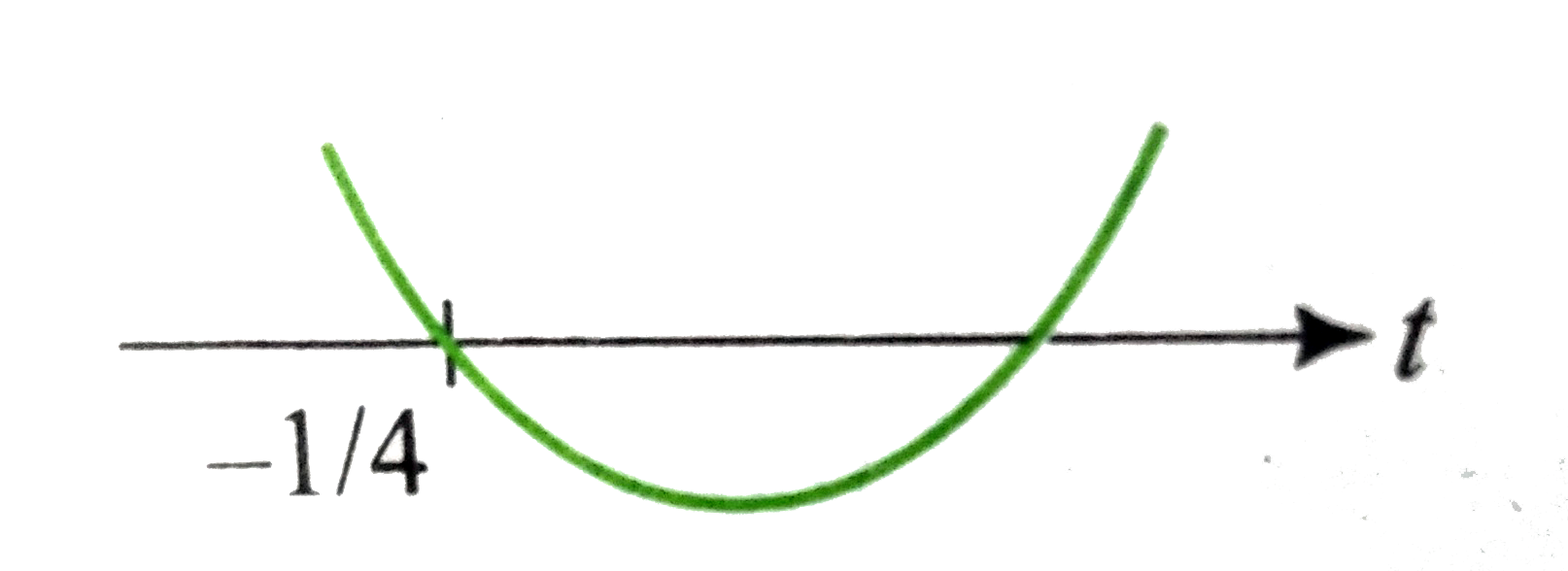
(i) D>0⇒|a|>4
(ii) f(−1/4)=0⇒a=65/4
(iii) −B2A>−14⇒a<12
No common solution.
∴a∈ϕ.
Topper's Solved these Questions
- THEORY OF EQUATIONSBOOK - CENGAGE PUBLICATIONCHAPTER - THEORY OF EQUATIONSEXERCISE - NUMERICAL VALUE TYPE
43 Videos
- THEORY OF EQUATIONSBOOK - CENGAGE PUBLICATIONCHAPTER - THEORY OF EQUATIONSEXERCISE - Archives JEE MAIN (single correct Answer Type )
7 Videos
- THEORY OF EQUATIONSBOOK - CENGAGE PUBLICATIONCHAPTER - THEORY OF EQUATIONSEXERCISE - Linked Comprechension Type
37 Videos
- STRAIGHT LINESBOOK - CENGAGE PUBLICATIONCHAPTER - STRAIGHT LINESEXERCISE - ARCHIVES (NUMERICAL VALUE TYPE)
1 Videos
- THREE DIMENSIONAL GEOMETRYBOOK - CENGAGE PUBLICATIONCHAPTER - THREE DIMENSIONAL GEOMETRYEXERCISE - All Questions
291 Videos
Similar Questions
If x=2+22/3+21/3 , then the value of x3−6x2+6x is
View SolutionIf the roots of the equation bx2+cx+a=0 be imaginary, then for all real values of x, the expression 3b2x2+6bcx+2c2 is (1) greater than 4ab (2) less than 4ab (3) greater than −4ab (4) less than 4ab
View SolutionConsider an unknow polynomial which divided by (x−3) and (x−4) leaves remainder 2 and 1, respectively. Let R(x) be the remainder when this polynomial is divided by (x−3)(x−4).
If equations R(x)=x2+ax+1 has two distint real roots, then exhaustive values of a are.
View SolutionFor a point P in the plane, let d1(P)andd2(P) be the distances of the point P from the lines x−y=0andx+y=0 respectively. The area of the region R consisting of all points P lying in the first quadrant of the plane and satisfying 2≤d1(P)+d2(P)≤4, is
View SolutionFind the angle between the line whose direction cosines are given by l+m+n=0andl2+m2−n2=0.
View SolutionIf a,b are the roots of x^(2)-10cx-11d=0 and c,a are roods of x^(2)-10ax-11b=0 then value of a+b+c+d is:
View SolutionIf the equation x^4 -λx^2 +9 has only two real roods, then the set of values of λ is
View SolutionWrite the roots of the following quadratic equations :
(i) (x−3)(x−4)=0 (ii) x2−x−2=0
View SolutionConsider the equation log22x−4log2x−m2−2m−13=0,m∈R. Let the real roots of the equation be x1,x2 such that x1<x2.
The sum of maximum value of, x1 and minimum value of x2 is :
View SolutionThe value of 'x' satisfying the equation x^(4)-2(x sin((pi)/(2)x))^(2)+1=0
View SolutionThe value of 'x' satisfying the equation x^(4)-2(x sin((pi)/(2)x))^(2)+1=0
View Solutionvalue of 'x' satisfying the equation x^(4)-2(x sin((pi)/(2)x))^(2)+1=0
View SolutionThe value of x ' satisfying the equation x^(4)-2(x sin((pi)/(2)x))^(2)+1=0
View Solutionபொருந்தாத ஒன்றை தேர்ந்தெடுக்க : சமன்பாட்டை நிறைவு செய்யும் ∣∣x2+3x∣∣+x2−2=0 x-ன் மதிப்புகள் .....................
View SolutionSolve the Equation:
(i) x2+3x+5=0
(ii) x2−x+2=0.
View SolutionFor the reaction Cl2+2I−→I2+2CI−, the initial concentration of I− was 0.20 mol lit−1 and the concentration after 20 min was 0.18 mol lit−1. If the rate of formation of I2 in mol lit−1min−1 is x×10−4 then the value of x is
View Solution
