Consider the circle x2+y2−8x−18y+93=0 with the center C and a point P(2,5) out side it. From P a pair of tangents PQ and PR are drawn to the circle with S as mid point of QR. The line joining P to C intersects the given circle at A and B. Which of the following hold (s)
CP is the arithmetic mean of AP and BP
PR is the geometric mean of PS and PC
PS is the harmonic mean of PA and PB
The angle between the two tangents from P is tan−1(43)
The correct Answer is:A, B, C, D
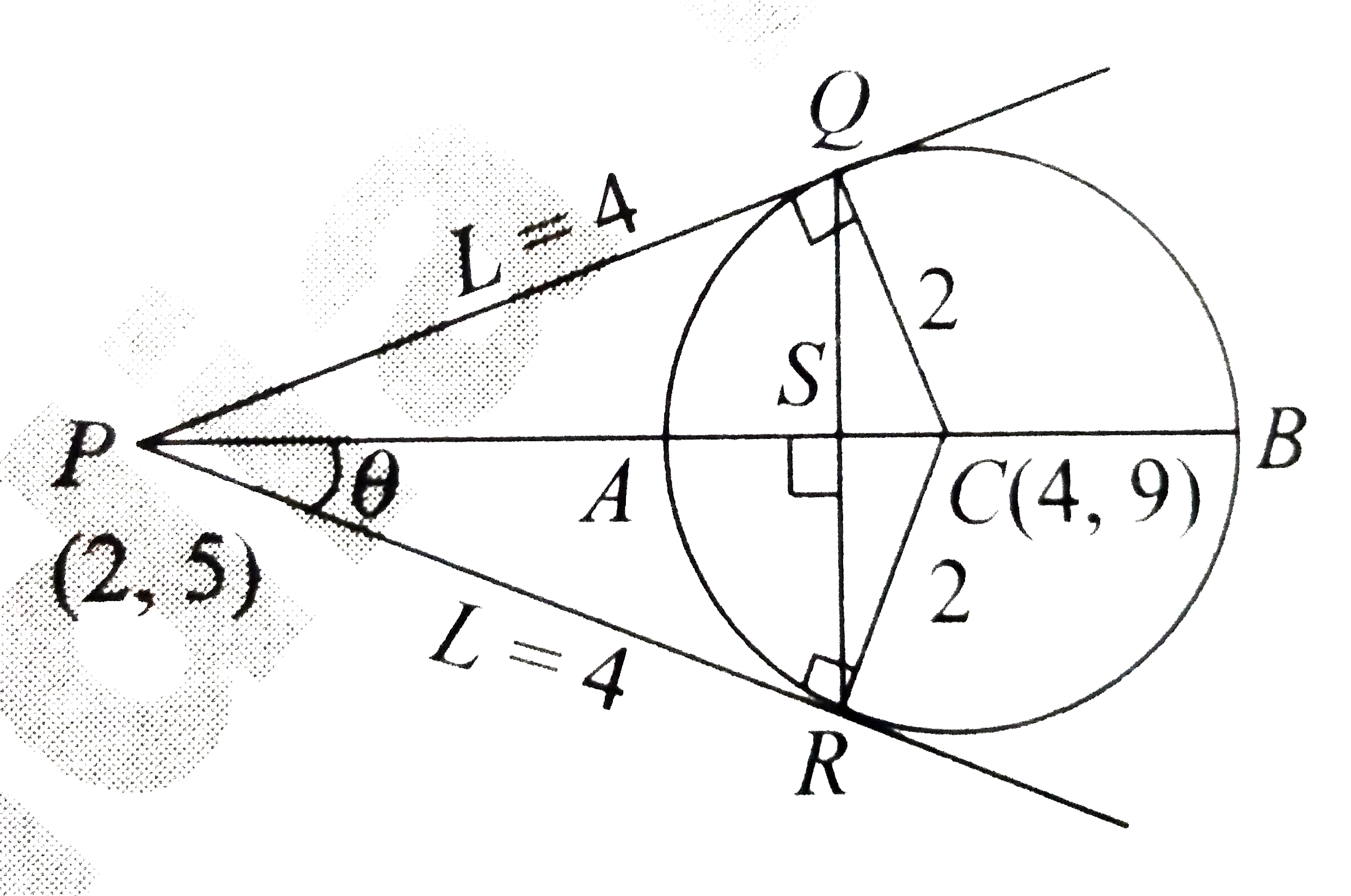
Radius =√16+81−93=2
CP=√20,AP=√20−2,BP=√20+2
⇒CP=AP+BP2
Thus, CP is the arithmetic mean of AP and BP
Now let, L=PR=√(PC)2−r2=√20−4=4=PQ
∴tanθ=24=12
Also, cosθ=PSPR
⇒PS=PRcosθ4.(2√5)=8√5
Harmonic mean between PA and PB
=2(√20−2)(√20+2)2√20=162√5=8√8=PS
Thus, PS is the harmonic mean of PA and PB.
(PS)(CP)=(8√5)(√20)=16=(PR)2
Thus, PR is the geometric mean of PS and CP.
Now, angle between the two tangents.
=2θ=2tan−1(12)=tan−1⎛⎝2.121−14⎞⎠=tan−1(43)
Topper's Solved these Questions
- CIRCLESBOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Comprehension Type
8 Videos
- CIRCLESBOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Single Correct Answer Type
58 Videos
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - JEE Advanced (Single Correct Answer Type)
14 Videos
- COMPLEX NUMBERSBOOK - CENGAGECHAPTER - COMPLEX NUMBERSEXERCISE - Question Bank
30 Videos
Similar Questions
Knowledge Check
From the point P(16,7), tangents PQ and PR are drawn to the circle x2+y2−2x−4y−20=0. If C is the centre of the circle, then area of quadrilateral PQCR is
A450 sq unitsB15 sq unitsC50 sq unitsD75 sq unitsFrom the point P(16, 7) tangents PQ and PR are drawn to the circle x2+y2−2x−4y−20=0. If c be the centre of the circle, then area of quadrilateral PQCR is
A450 sq unitB15 sq unitC50 sq unitD75 sq unitTangents to a circle at points P and Q on the circle intersect at a point R. If PQ= 6 and PR= 5 then the radius of the circle is
A133B4C154D165
Let P be a variable point. From P tangents PQ and PR are drawn to the circle x2+y2=b2 if QR always touch the parabola y2=4ax then locus ofP is
View SolutionFrom the point P(16,7), tangents PQ and PR are drawn to the circle x2+y2−2x−4y−20=0 If C is the centre of the circle, then area of quadrilateral PQCR is
View SolutionIf from a point P, tangents PQandPR are drawn to the ellipse x22+y2=1 so that the equation of QR is x+3y=1, then find the coordinates of P.
View Solution
A point P is 13 cm from the centre of the circle. The two tangent PQ and PR are drawn from the point P, The length of the tangent drawn from P to the circle is 12 cm.
Find the radius of the circle.
View SolutionTangents are drawn to the circle x2+y2=16 at the points where it intersects the circle x2+y2−6x−8y−8=0, then the point of intersection of these tangents is
View Solution
