Consider the ellipse whose major and minor axes are x-axis and y-axis, respectively. If $ϕ$ is the angle between the CP and the normal at point P on the ellipse, and the greatest value $tan ϕ$ is $\frac{3}{4}$ (where C is the centre of the ellipse). Also semi-major axis is 10 units . The eccentricity of the ellipse is

$1 / 2$

$1 / 3$

$\sqrt{3} / 2$

none of these

Video Solution

Text Solution

Verified by Experts

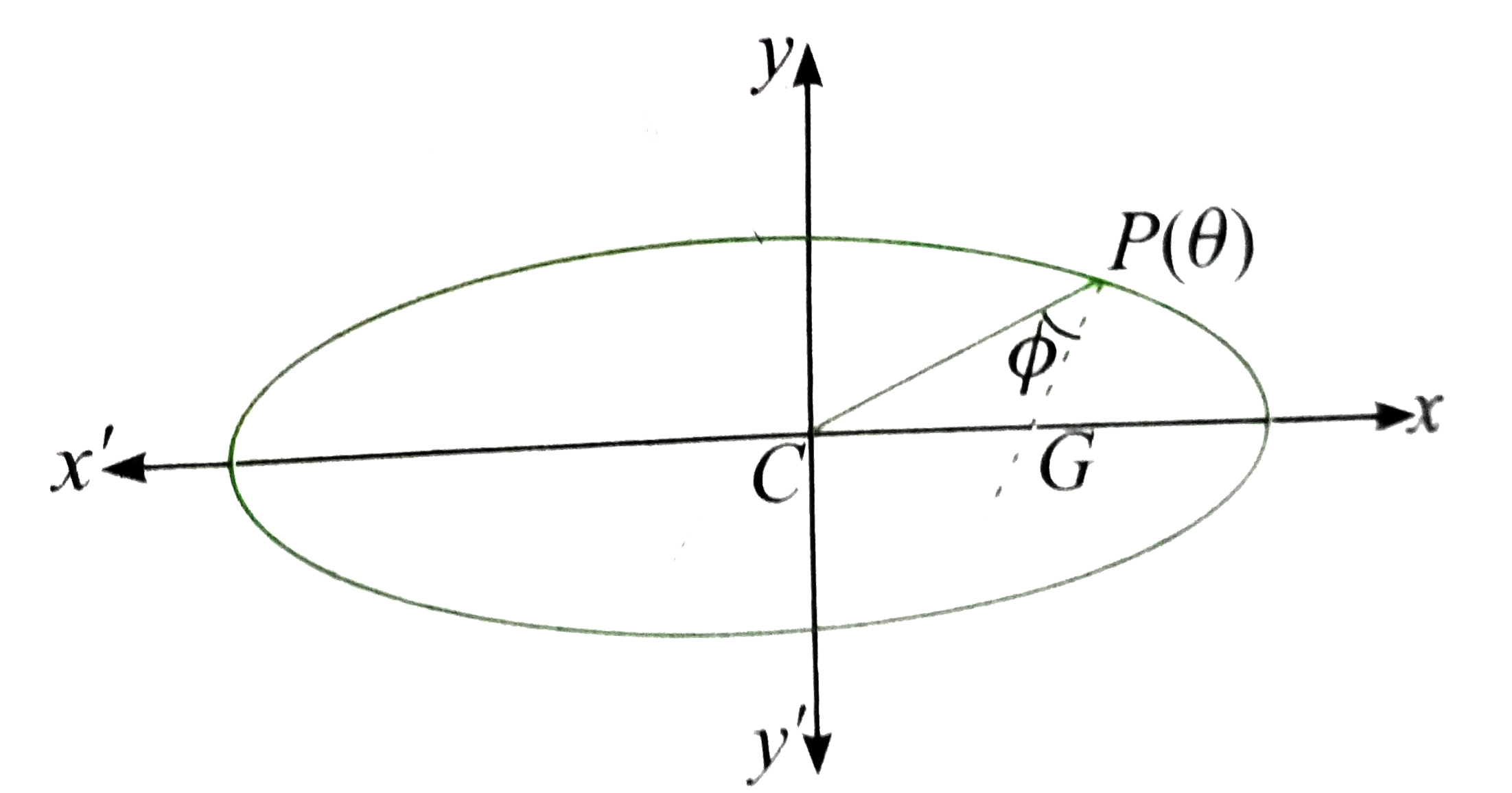
Let P be any point on the ellipse t $(a cos θ, b sin θ)$
Therefore, the equation of CP is
$y = (\frac{b}{a} tan θ) x$
The normal to the ellipse at P is
$\frac{a x}{cos θ} - \frac{b x}{sin θ} = a^{2} - b^{2}$
Slopes of the lines CPand the normal GP are (b/a) $tan θ$ and (a/b) $tan, θ$ respectively. Therefore,
$tan ϕ = \frac{\frac{a}{b} tan θ - \frac{b}{a} tan θ}{1 + \frac{a}{b} tan θ \frac{b}{a} tan θ}$
$\frac{a^{2} - b^{2}}{a b} = \frac{tan θ}{{sec}^{2} θ}$
$= \frac{a^{2} - b^{2}}{a b} sin θ cos θ = \frac{a^{2} - b^{2}}{2 a b} sin 2 θ$
Therefore , the greatest value of $tan ϕ$ is
$\frac{x^{2} - b^{2}}{2 a b} \times 1 = \frac{a^{2} - b^{2}}{2 a b}$
Given that
$\frac{a^{2} - b^{2}}{2 a b} = \frac{3}{2}$
Let $\frac{a}{b} = t$
$∴ t - \frac{1}{t} = \frac{3}{2}$
or $2 t^{2} - 3 t - 2 = 0$
$or 2 t^{2} - 4 t + t - 2 = 0$
$or (2 t + 1) (t - 2)$
$\frac{a}{b} = 2$
or $e^{2} = 1 - \frac{1}{4}$
or $e = \frac{\sqrt{3}}{2}$
The rectangle inscribed in the ellipse, whose one vertexis $a (cos θ, b sin θ), is (2 a cos θ b sin θ) = 2 a b sin (2 θ)$ which has maximum, value 2ab. Given that a=10. Then b=5. Therefore, the maximum area is 100

Updated on:21/07/2023