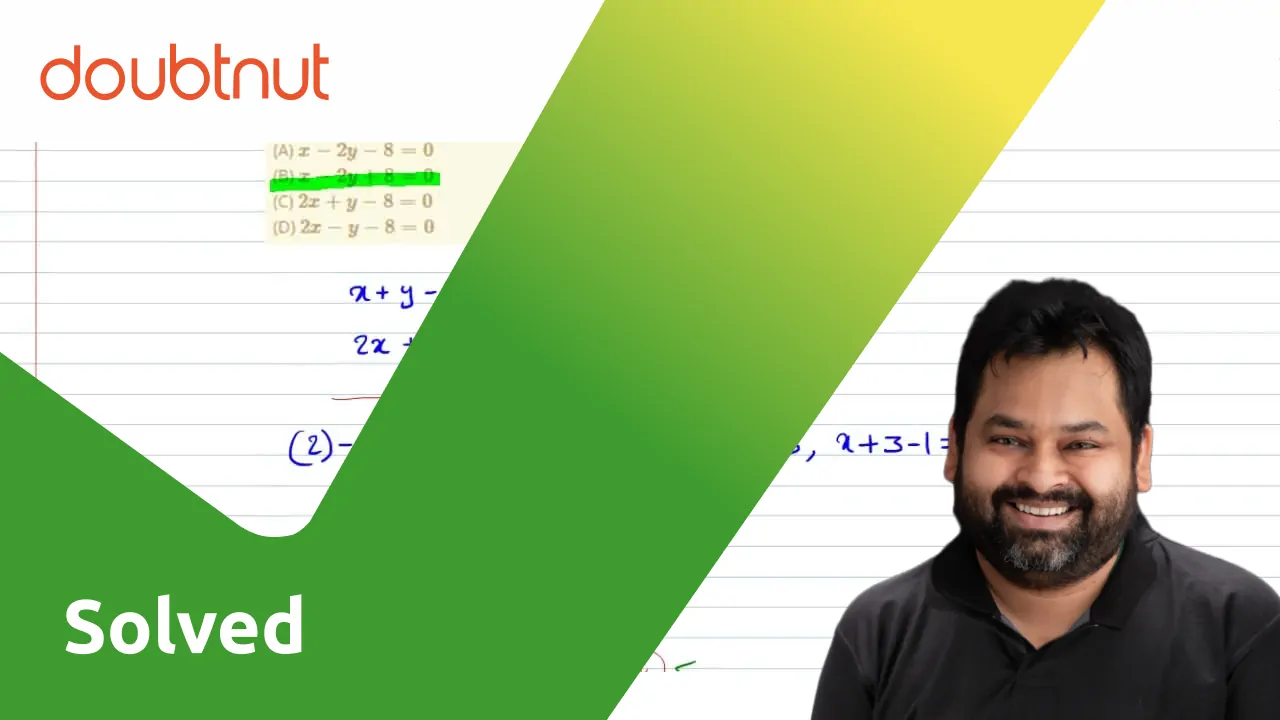
Consider the family of lines (x+y−1)+λ(2x+3y−5)=0 and (3x+2y−4)+μ(x+2y−6)=0. Equation of a line that belongs to both the family is
(A) x−2y−8=0
(B) x−2y+8=0
(C) 2x+y−8=0
(D) 2x−y−8=0
First, we will solve equations,
x+y−1=0→(1) and 2x+3y−5=0→(2)
Multiplying (1) by 2 and subtracting it from (2), we get,
2x+3y−2x−2y=5−2⇒y=3
Putting y=3 in (1),
x+3−1=0⇒x=−2
So, point of intersection of first family of line is (−2,3).
Now, we will solve equations,
3x+2y−4=0→(3) and x+2y−6=0→(4)
Subtracting (4) from (3), we get,
3x+2y−x−2y=4−6⇒x=−1
Putting x=−1 in (4),
−1+2y−6=0⇒y=72
So, point of intersection of second family of line is (−1,72).
Now, ,using slopes we can find the equation of the required line,
y−3x−(−2)=72−3−1−(−2)
⇒y−3x+2=12⇒2y−6=x+2
⇒x−2y+8=0, which is the required equation.
Similar Questions
रेखाओं के कुल (x+y−1)+λ(2x+3y−5)=0 तथा (3x+2y−4)+μ(x+2y−6)=0, पर विचार कीजिए। दोनों कुलों से सम्बन्धित सरल रेखा की समीकरण है
06:02View SolutionThe lines x+2y+3=0,x+2y−7=0,and2x−y−4=0 are the sides of a square. The equation of the remaining side of the square can be (a) 2x−y+6=0 (b) 2x−y+8=0 (c) 2x−y−10=0 (d) 2x−y−14=0
02:41View SolutionThe lines x+2y+3=0,x+2y−7=0,and2x−y−4=0 are the sides of a square. The equation of the remaining side of the square can be 2x−y+6=0 (b) 2x−y+8=0 2x−y−10=0 (b) 2x−y−14=0
02:22View SolutionThe point of intersection of the diagonals of the rhombus formed by the lines 2x+y−5=0,x+2y+8=0,2x+y+5=0, and x+2y−2=0 is
03:54View SolutionConsider the family of lines (x+y−1)+λ(2x+3y−5)=0 and (3x+2y-4)+μ(x+2y−6)=0, equation of a straight line that belongs to both the families is
04:46View SolutionConsider the family of line (x+y−1)+λ(2x+3y−5)=0 and (3x+2y−4)+μ(x+2y−6)=0 Equation of a straight line that belongs to both the families is:
04:04View SolutionThe equation of the tangent to the curve x2−2xy+y2+2x+y−6=0 at (2,2) is a)2x+y−6=0 b)2y+x−6=0 c)x+3y−8=0 d)3x+y−8=0
04:32View SolutionThe lines x+2y+3=0,x+2y−7=0,and2x−y−4=0 are the sides of a square. The equation of the remaining side of the square can be (a) 2x−y+6=0 (b) 2x−y+8=0 (c) 2x−y−10=0 (d) 2x−y−14=0
05:41View Solution