Consider the function $f (x) = {\begin{matrix} x - [x] - \frac{1}{2} & x \notin 0 & x \in I \end{matrix}$ where [.] denotes the fractional integral function and I is the set of integers. Then find $g (x) max . [x^{2}, f (x), | x |}, - 2 \leq x \leq 2 .$

Video Solution

Text Solution

Verified by Experts

Clearly, from graph,

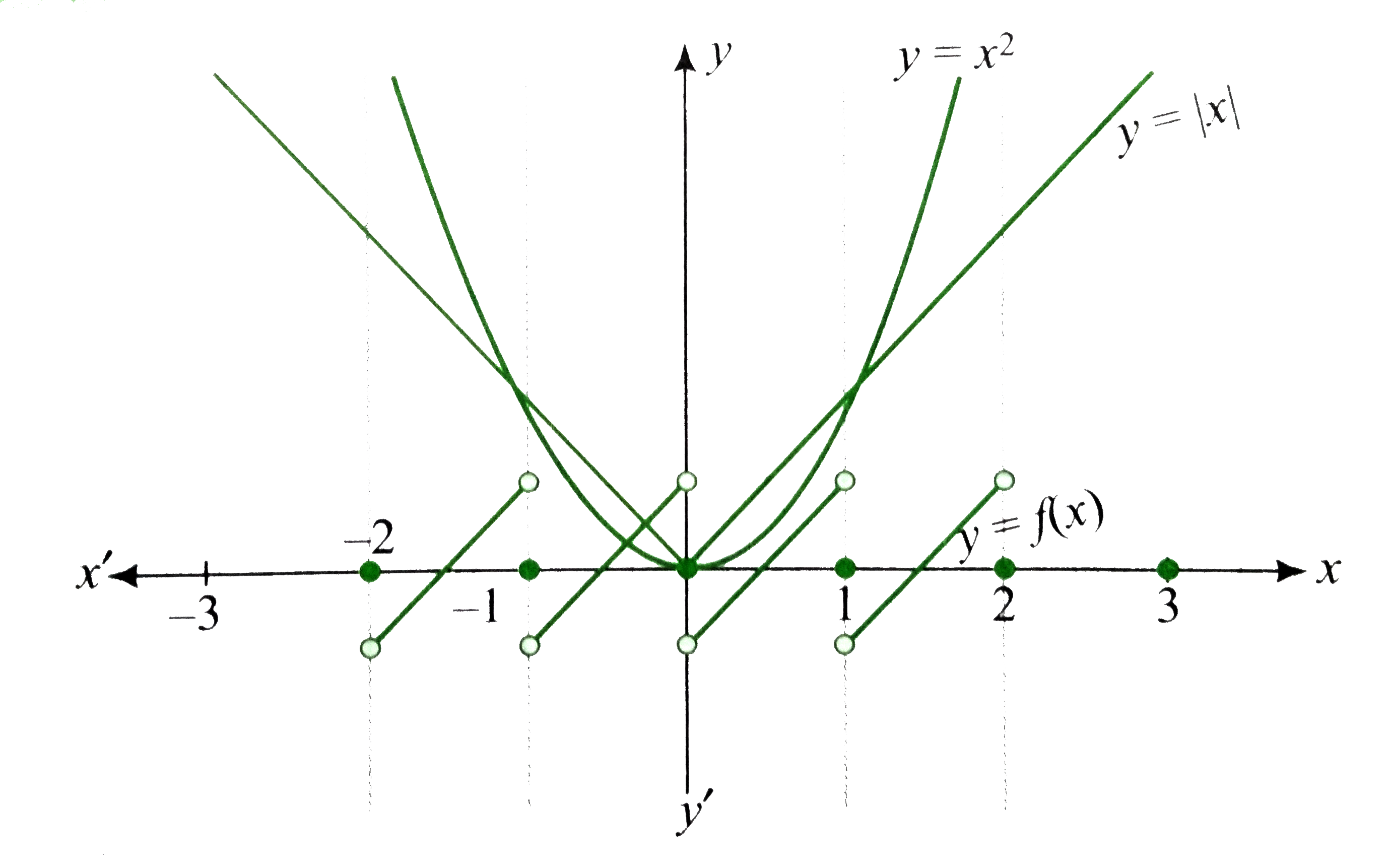
$g (x) = ⎧ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎩ \begin{matrix} x^{2}, & - 2 \leq x \leq - 1 - x, & - 1 < x \leq - 1 / 4 \frac{1}{2} + x, & - \frac{1}{4} < x < 0 x, & 0 \leq x < 1 x^{2}, & 1 \leq x < 2 \end{matrix}$

Updated on:21/07/2023

$if f (x) = {\begin{matrix} 2 x - [x] + sin (x - [x]) & x \neq 0 0 & x - 0 \end{matrix}$ where [.] denotes the greatest integer function then
Af(X) is differentiable at x=0
Bf(x) is differentiable at x=2
Cf(x) is continuous but not differentiable at x=0
Dnone of these
The domain of function $f (x) = {log}_{[x + \frac{1}{2}]} (2 x^{2} + x - 1),$ where $[.]$ denotes the greatest integer function is :
A $[\frac{3}{2}, \infty)$
B $(2, \infty)$
C $(- \frac{1}{2}, \infty) - {\frac{1}{2}}$
D $(\frac{1}{2}, 1) \cup (1, \infty)$
The function $f (x) = [x] + \frac{1}{2}, x \notin I$ is a/an (wher [.] denotes greatest integer function)
AEven
Bodd
Cneither even nor odd
Deven as well as odd