Consider the integral I=∫π0xsinx1+cos2xdx
Express I=π2∫π0sinx1+cos2xdxSolution in Malayalam
Step by step video & image solution for Consider the integral I=int_0^pi(xsinx)/(1+cos^2x)dx Express I=pi/2int_0^pisinx/(1+cos^2x)dx by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
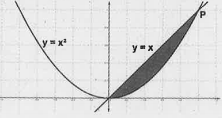
Consider the following figure
find the point of intersection (P) of the parabola and the line.
View SolutionEvaluate: ∫π0xsinx1+cos2xdx
View SolutionEvaluate (i) int_0^(pi//4) sin x cos x dx (ii) int_0^(pi//2) (1 + cos x)^(1//2) dx (iii) int_0^(pi//2) (1 + sin x)^(1//2) dx (iv) int_0^(pi//4) (1 -cos 2x)^(1//2)dx
View SolutionEvalute: ∫π0xsinx1+cos2xdx.
View Solution∫π0(cos2x)dx,
View Solutionপ্রমান করো: ∫π0xsinx1+cos2xdx=π24
View SolutionEvaluate: ∫π0xsinx1+cos2x dx
View SolutionEvaluate: ∫π0xsinx1+cos2x dx
View SolutionFind the mistake in the following evaluation of the integral I=∫π0dx1+2sin2x, then : I=∫π0dxcos2x+3sin2x =∫π0sec2xdx1+3tan2x=1√3[tan−1(√3tanx)]0π=0
View SolutionEvaluate: ∫π0xsinx1+cos2x dx
View SolutionEvaluate: ∫π0xsinx1+cos2xdx
View SolutionEvaluate ∫π0xsinx1+cos2xdx
View SolutionEvaluate : ∫π0xsinx1+cos2xdx.
View SolutionConsider the integral I=∫π0xsinx1+cos2xdx
Show that I=π24
View SolutionEvaluate ∫π0xsinx1+cos2xdx
View Solution
