Consider the linear equations .
Match the conditions/expressions in Column I with statements in Column II.

The correct Answer is:
Here we have the determinant of the coefficient matrix of given equation as
a.
and
or
or
Therefore, this question represents identical planes.
b.
and
This means are not all equal. Therefore, all equations are not identical but have infinite solutions. Hence,
(using )
and
rArr
Therefore, the equations represent the line .
c.
and the equations have only trivial solution, i.e., .
Therefore, the equations represent the planes meeting at a single point, namely origin.
d.
All equations are satisfied by all .
The equations represent the whole of the three-dimensional space.
Topper's Solved these Questions
- BOOK - CENGAGE ENGLISHCHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - ARCHIVES INTEGER TYPE1videos
THREE-DIMENSIONAL GEOMETRY
- BOOK - CENGAGE ENGLISHCHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - ARCHIVES LINKED COMPREHENSION TYPE3videos
THREE-DIMENSIONAL GEOMETRY
- BOOK - CENGAGE ENGLISHCHAPTER - THREE DIMENSIONAL GEOMETRYEXERCISE - All Questions294videos
THREE DIMENSIONAL GEOMETRY
- BOOK - CENGAGE ENGLISHCHAPTER - TRIGONOMETRIC EQUATIONSEXERCISE - Archives (Matrix Match Type)1videos
TRIGONOMETRIC EQUATIONS
Similar Questions
Match the conditions/ expressions in Column I with statement in Column II
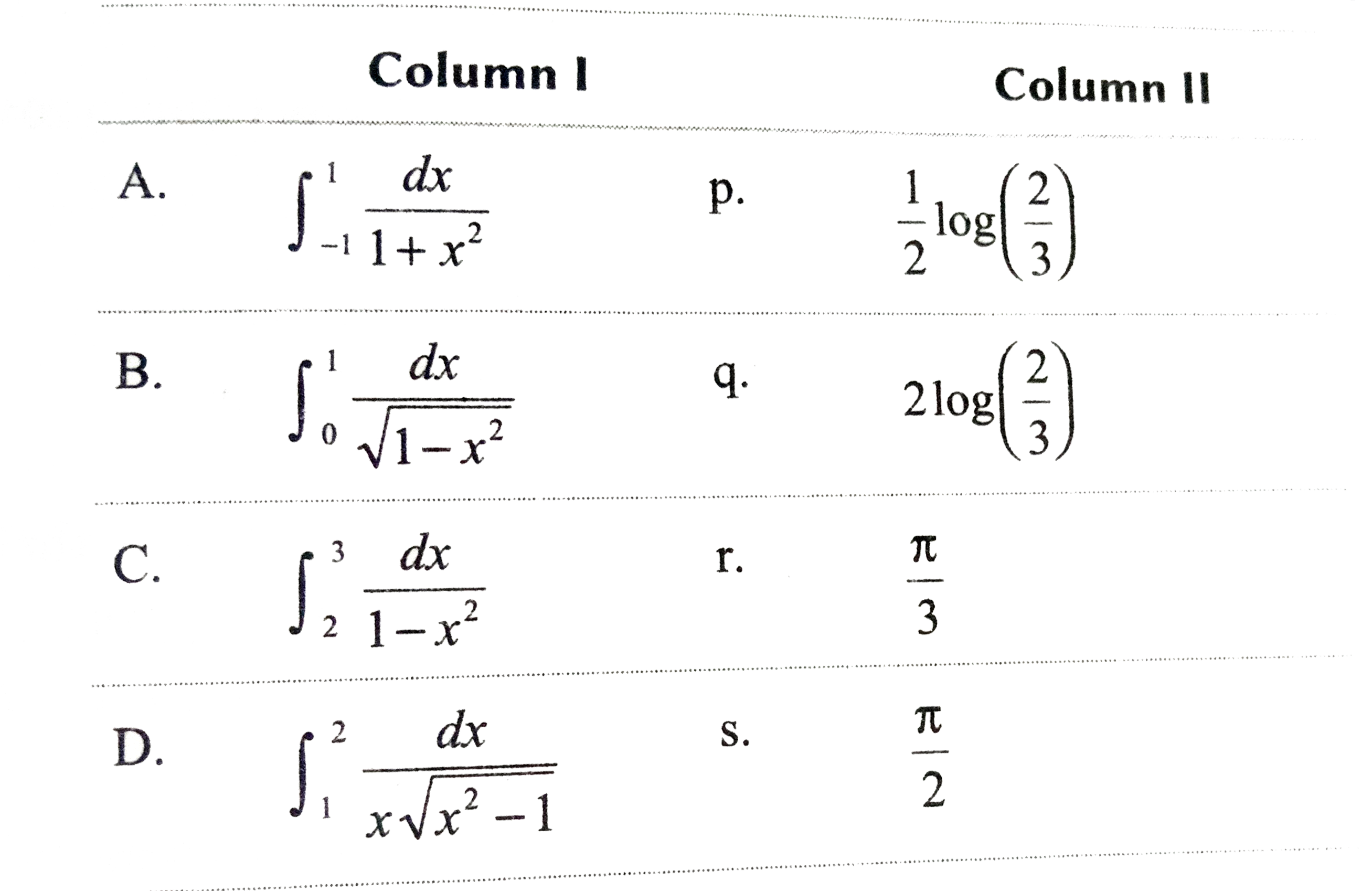 View Solution
View SolutionMatch the conditions / expression in Column I with statement in Column II.
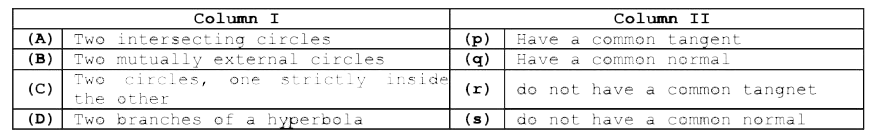 View Solution
View SolutionMatch the reactions given in Column I with the statements given in Column II
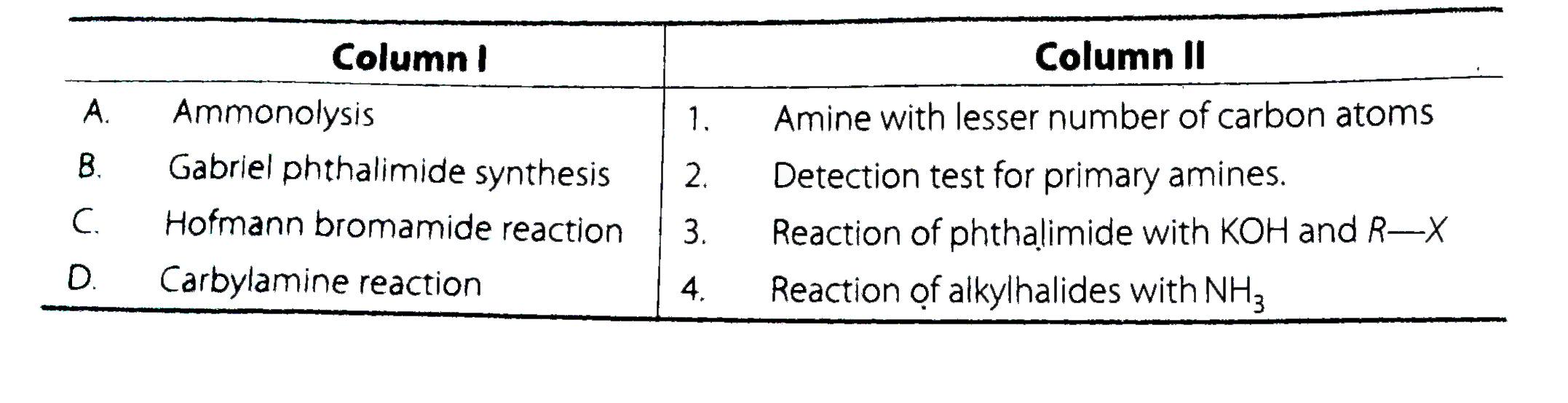 View Solution
View SolutionMatch the reactions given in Column I with the statements given in Column II
 View Solution
View SolutionMatch the entries in column II with the statements given in column I.
 View Solution
View SolutionMatch the statements in Column I with the currnt element in Column II
 View Solution
View Solutionmatch the types of defect given in column I with the statement given in column II.
 View Solution
View SolutionMatch the statement given in Column I with the phenomenon given in Column II.
 View Solution
View Solutionmatch the types of defect given in column I with the statement given in column II.
 View Solution
View SolutionMatch the statement in Column I to the approprate statement(s) from Column II.
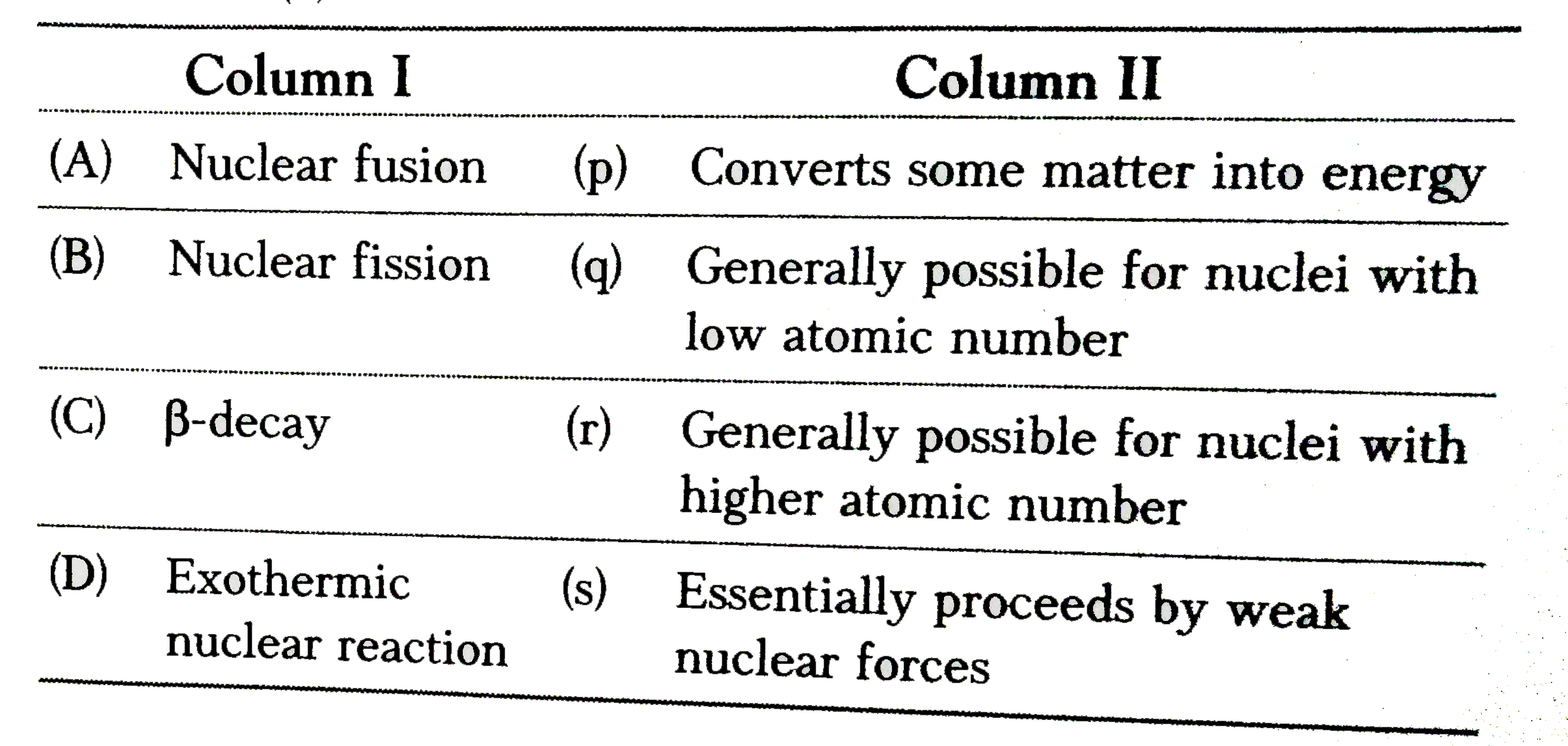 View Solution
View Solution

