Consider the points $A (0, 1) a n d B (2, 0), a n d P$ be a point on the line $4 x + 3 y + 9 = 0$ . The coordinates of $P$ such that $| P A - P B |$ is maximum are $(- \frac{12}{5}, \frac{17}{5})$ (b) $(- \frac{84}{5}, \frac{13}{5})$ $(\frac{31}{7}, \frac{31}{7})$ (d) $(, 0)$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

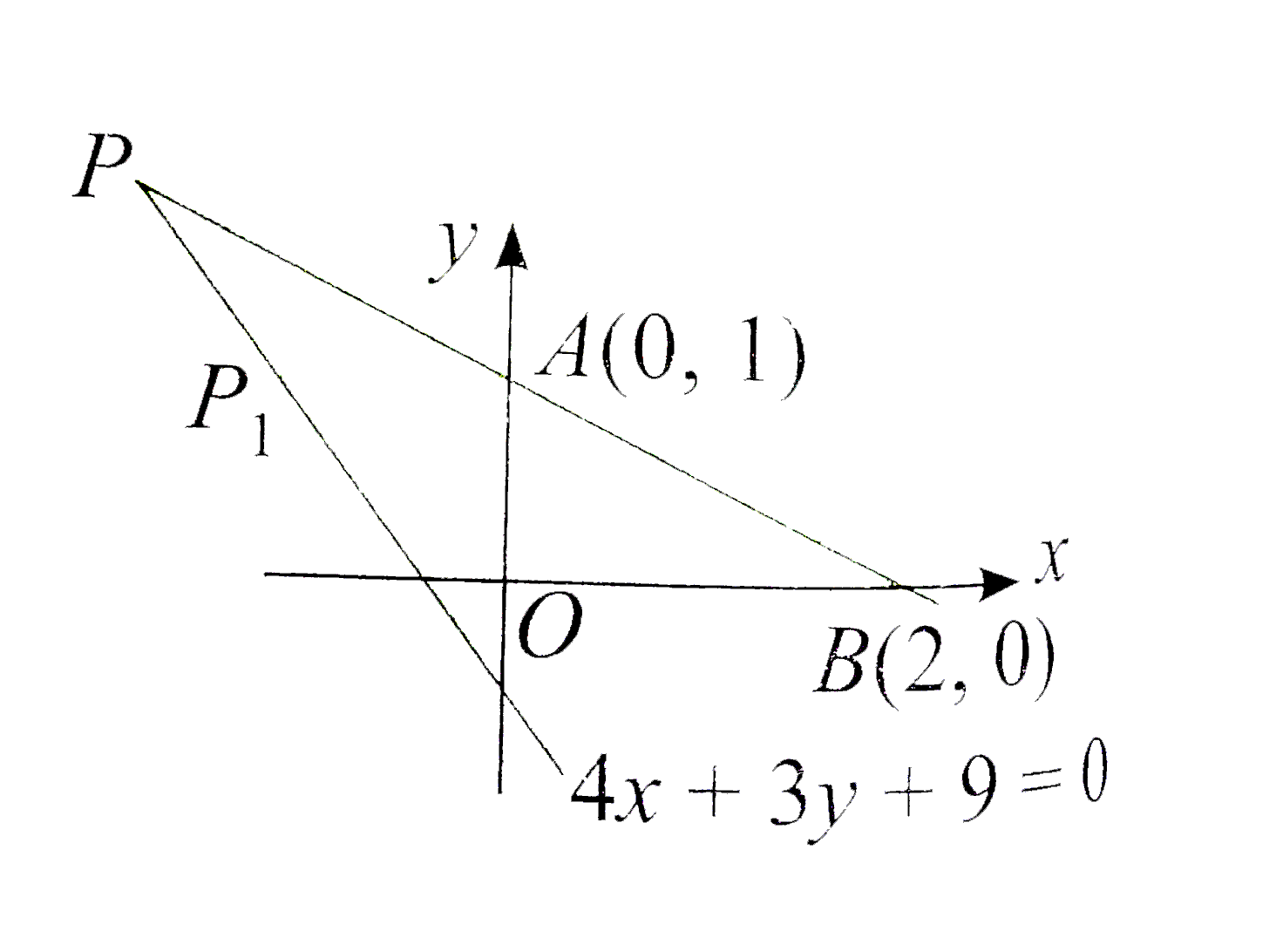
The equation of AB is
$y - 1 = \frac{0 - 1}{2 - 1} x or x + 2 y - 2 = 0$
$| P A - P B | \leq A B$
Thus, |PA-PB| is maximum if the points A,B, and P are collinear.
Hence, solving x+2y-2=0 and 4x+3y+9=0, we get point $P \equiv (- 24 / 5, 17 / 5) .$

|

Updated on:21/07/2023

Class 12 MATHS STRAIGHT LINES

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Statement I Let $A \equiv (0, 1) and B \equiv (2, 0)$ and P be a point on the line $4 x + 3 y + 9 = 0$ then the co - ordinates of P such that $| P A - P B |$ is maximum is $(- \frac{12}{5}, \frac{17}{5})$
Statement II $| P A - P B | \leq | A B |$
AStatement I is true ,statement II is true , statement II is a correct explanation for statement I
BStatement I is true ,statement II is true statement II is not a correct explanation for statement I
CStatement I is true ,statement II is false
DStatement I is false ,statement II is true
Question 2 - Select One
If $A (3, 1) and B (- 5, 7)$ are any two given points, If P is a point one the line $y = x$ such that $P A + P B$ is minimum then P is
A $(1, 1)$
B $(11 / 5, 11 / 5)$
C $(7 / 13), 7 / 13)$
Dnone of these
Question 3 - Select One
The point P(a,b) and Q(b,a) lie on the lines $3 x + 2 y - 13 = 0$ and $4 x - y - 5 = 0$ . The equation of line PQ is
A $x - y = 5$
B $x + y = 5$
C $x - y = - 5$
D $x + y = - 5$

CENGAGE-STRAIGHT LINES-Exercise (Single)

Home
Ask Doubt
Profile