Consider the sequence of natural numbers S0,S1,S2,... such that S0=3,S1=3andSn=3+Sn−1Sn−2, thenSolution in Bengali
A. S1545 is odd and S1546 is even.
B. S1545 is even and S1546 is odd.
C. both S1545 and S1546 are even.
D. both S1545 and S1546 are odd.
The correct Answer is:C
Since −1≤sinx≤1, the curve y=e−xsinx is bounded by the curve y=e−xandy=e−x.
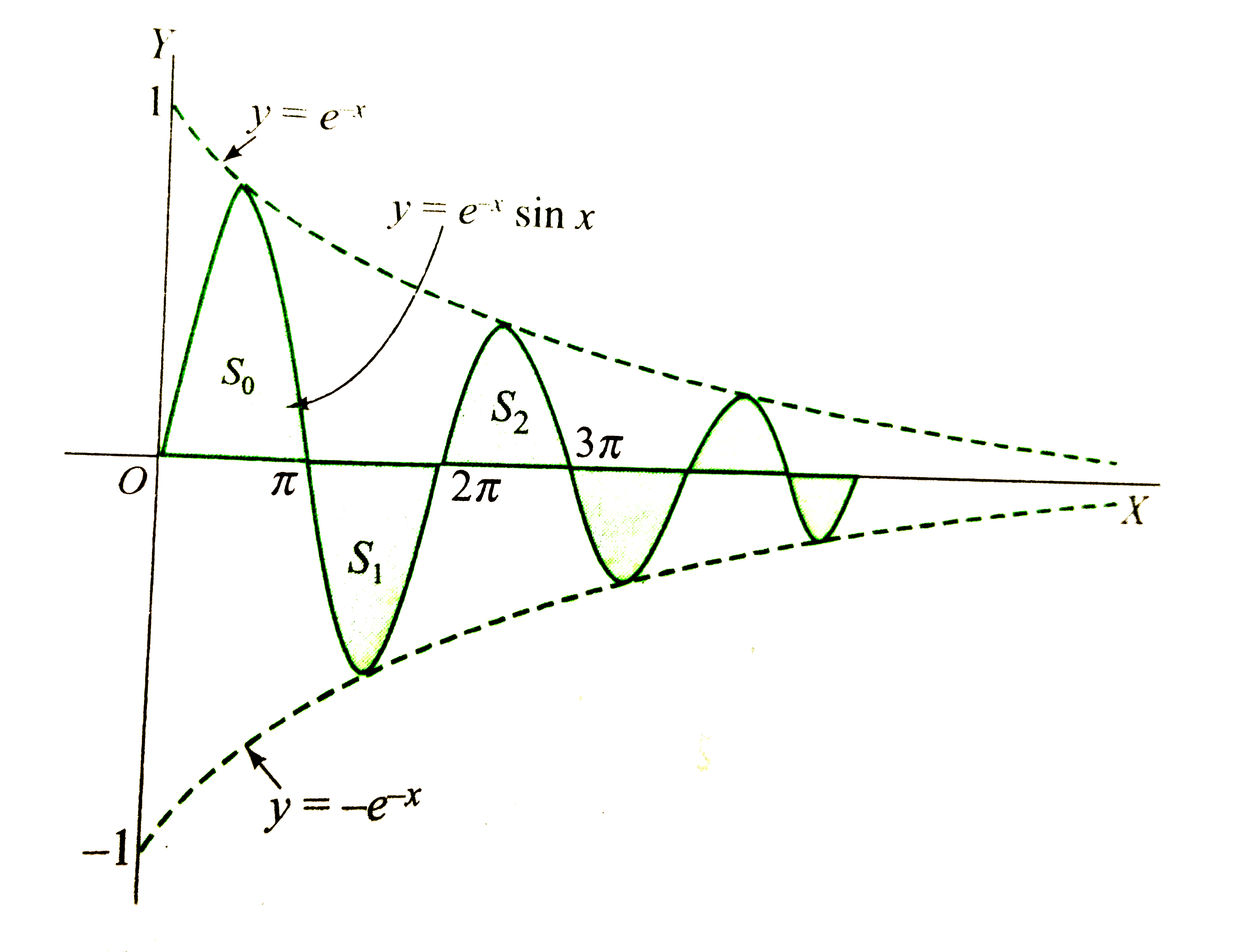
Also, the curve y=e−xsinx intersects the positive semi-axis OX at the points where sin x=0, where xn=nπ,n∈Z.
Also |yn|=|y coordinate in the half-wave Sn|
∴ Sn=(−1)n(n+1)π∫nπe−xsinxdx
=(−1)n+12[e−x(−sinx+cosx)](n+1)πnπ
=(−1)n+12[e−(n+1)x(−1)n+1−enπ(−1)n]
=e−nπ2(1+eπ)
⇒ Sn+1Sn=e−π
and S0=12(1+eπ).
Therefore, the sequence S0,S1,S2,... forms an infinite G.P. with common ratio e−π. we have
∞Σn=0Sn=12(1+eπ)1−e−π
Topper's Solved these Questions
- AREABOOK - CENGAGE PUBLICATIONCHAPTER - AREAEXERCISE - Matrix Match Type
5 Videos
- AREABOOK - CENGAGE PUBLICATIONCHAPTER - AREAEXERCISE - Numerical Value Type
18 Videos
- AREABOOK - CENGAGE PUBLICATIONCHAPTER - AREAEXERCISE - Multiple Correct Answers Type
13 Videos
- APPLICATIONS OF DERIVATIVESBOOK - CENGAGE PUBLICATIONCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Subjective Type
2 Videos
- BINOMIAL THEOREMBOOK - CENGAGE PUBLICATIONCHAPTER - BINOMIAL THEOREMEXERCISE - Comprehension
11 Videos
Similar Questions
Match the following lists :

View SolutionThe area enclosed by the curve c:y=x√9−x2(x≥0) and the x-axis is________
View SolutionLet A(k) be the area bounded by the curves y=x2−3 and y=kx+2 The range of A(k) is (10√53,∞) The range of A(k) is (20√53,∞) If function k→A(k) is defined for k∈[−2,∞ ), then A(k) is many-one function. The value of k for which area is minimum is 1.
View SolutionProve that for λ>1, the equation xlogx+x=λ has least one solution in [1,λ].
View SolutionConsider a G.P. with first term (1+x)n, |x|<1, common ratio 1+x2 and number of terms (n+1). Let 'S' be sum of all the terms of the G.P., then
The coefficient of xn is 'S' is
View SolutionIf S_1,S_2,S_3,...,S_n be the sums of first n terms of n G.P.'s whose first terms are each unity and the common ratios are 1, 2, 3,.....,n respectively, prove that S_1+S_2+2S_3+3S_4+.........+(n-1)S_n=1^n+2^n+3^n+....+n^n.
View SolutionConsider the sequence of natural numbers s_(0),s_(1),s_(2),... such that s_(0)=3,s_(1)=3 and s_(n)=3+s_(n-1)s_(n-2) then
View SolutionIf sum of n terms of a sequence is Sn then its nth term tn=Sn−Sn−1. This relation is valid for all n>−1 provided S0=0. But if S1=0, then the relation is valid only for n≥2 and in hat cast t1 can be obtained by the relationt1=S1. Also if nth term of a sequence t1=Sn−Sn−1 then sum of n term of the sequence can be obtained by putting n=1,2,3,.n and adding them. Thus n∑n=1tn=Sn−S0. if S0=0,thenn∑n=1tn=Sn. On the basis of above information answer the following questions: If the sum of n terms of a sequence is 10n2+7n then the sequence is (A) an A.P. having common difference 20 (B) an A.P. having common difference 7 (C) an A.P. having common difference 27 (D) not an A.P.
View Solutionयदि किसी समान्तर श्रेढ़ी के n पदों का योग Sn हो तथा S1=6, और S7=105, तो सिद्ध कीजिए की Sn:Sn−3=(n+3):(n−3) .
View SolutionLet Sn=cos(nπ10),n=1,2,3,…… then the value of s1s2……s10s1+s2+……..+s10 is equal to
View SolutionFor any natural number n the sets S1,S2,….. are defined as below:
S1={1}.S2={2,3},S3={4,5,6}
S4={7,8,9,10},S5={11,12,13,14,15}: etc.
The last element in the S24 is :
View SolutionFor any natural number n the sets S1,S2,….. are defined as below:
S1={1}.S2={2,3},S3={4,5,6}
S4={7,8,9,10},S5={11,12,13,14,15}: etc.
The middlemost element of the set S15 is:
View SolutionFor any natural number n the sets S1,S2,….. are defined as below:
S1={1}.S2={2,3},S3={4,5,6}
S4={7,8,9,10},S5={11,12,13,14,15}: etc.
The sum of the elements of set S25 is :
View SolutionFor any natural number n the sets S1,S2,….. are defined as below:
S1={1}.S2={2,3},S3={4,5,6}
S4={7,8,9,10},S5={11,12,13,14,15}: etc.
On which set the sum of all the elements of the set is even :
View SolutionIf S1,S2,S3 are the sum of first n natural numbers, their squares and their cubes, respectively , show that 9S22=S3(1+8S1)
View SolutionIf S1,S2,S3 are the sum of first n natural numbers, their squares and their cubes, respectively , show that 9S22=S3(1+8S1)
View Solution
