Consider the two 'Postulates' given below.
(i) Given any two distinct points A and B , there exists a third point C , which is between A and B . Solution in Kannada
Step by step video & image solution for Consider the two 'Postulates' given below. (i) Given any two distinct points A and B , there exists a third point C , which is between A and B . by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A park, in the shape of a quadrilateral ABCD, has C=90∘, AB = 9 m, BC = 12 m, CD = 5 m and AD = 8m.
How much area does it occupy?
View SolutionGive geometric representation of y=3 as an equation
in one variable
View SolutionConsider two ‘postulates’ given below:(i) Given any two distinct points A and B, there exists a third point C which is in between A and B.(ii) There exist at least three points that are not on the same line. Do these postulates contain any undefined terms? Are these postulates consistent? Do they follow from Euclid’s postulates? Explain.
View SolutionIf a and b are two distinct real roots of the polynomial f(x) such that a
View SolutionShow that the difference of any two sides of a triangle is less than the third side. Given : A ABC To Prove: (i) AC−AB<BC BC−AC<AB (iii) BC−AB<AC Construction: Take point D on AC such that AD=AB . Join BD
View Solutionनीचे दी हुई दो अभिधारणाओं पर विचार कीजिए :
(i) दो भिन्न बिंदु A और B दिए रहने पर, एक तीसरा बिंदु C ऐसा विद्यमान है जो A और B के बीच स्थिति होता है |
(ii) यहां कम से कम ऐसे तीन बिंदु विद्यमान हैं कि वे एक रेखा पर स्थित हैं |
क्या इस अभिधारणाओं में कोई अपरिभाषित शब्द हैं ? क्या ये अभिधारणाएँ अविरोधी हैं ? क्या ये यूक्लिड की अभिधारणाओं से प्राप्त होती है ? स्पष्ट कीजिए |
View Solutionनीचे दी हुई दो अभिधारणाओं पर विचार कीजिए:
(i) दो भिन्न बिन्दु A और B दिए रहने पर, एक तीसरा बिन्दु C ऐसा विद्यमान है जो A और B के बीच स्थित होता है।
(ii) यहाँ कम-से-कम ऐसे तीन विन्द विद्यमान हैं कि वे एक रेखा पर स्थित नहीं हैं। क्या इन अभिधारणाओं में कोई अपरिभाषित शब्द हैं? क्या ये अभिधारणाएँ अविरोधी हैं? क्या ये यूक्लिड की अभिधारणाओं से प्राप्त होती हैं? स्पष्ट कीजिए।
View Solutionनीचे दी हुई अभिधारणा पर विचार कीजिए :
दो भिन्न बिंदु A और B दिए रहने पर , एक तीसरा बिंदु C ऐसा विद्यमान हैं जो A और B के बीच स्थित होता हैं ।
क्या इस अभिधारणा में कोई अपरिभाषित शब्द हैं ? क्या ये अभिधारणाएँ अविरोधी हैं ? क्या ये यूक्लिड की अभिधारणाओं से प्राप्त होती हैं स्पष्ट कीजिए ।
View SolutionConsider the two 'Postulates' given below.
(ii) There exists at least three points that are not on the same line
Do these postulates contain any undefined terms ? Do they follow from Euclid's postulates ? Explain.
View Solutionनीचे दी गई अभिधारणाओं पर विचार कीजिए :
दो भिन्न बिन्दु A और B दिए रहने पर एक तीसरा बिन्दु C ऐसा विघमान है जो A और B के बीच स्थित होता है।
View SolutionConsider the two 'postulates' gives below:
(i) Given any two distinct points A and B, there exists a third point C, which is between A and B.
(ii) There exist at least three points that are not on the same line.
Do these postulates contain any undefined terms? Are these postulates consistent? Do they follow from Euclid's postulates? Explain.
View SolutionConsider two ‘postulates’ given below:(i) Given any two distinct points A and B, there exists a third point C which is in between A and B.(ii) There exist at least three points that are not on the same line. Do these postulates contain any undefined terms? Are these postulates consistent? Do they follow from Euclid’s postulates? Explain.
View Solutionनीचे दिय गए चित्र में अपरिवर्ति धारा में बिन्दुओं A तथा B तथा बिन्दुओं B तथा C के बीच विभवान्तर क्रमशः है।
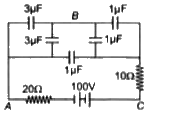
View SolutionConsider ‘postulate’ given below. Given any two distinct points A and B, there exists a third point C which is between A and B. Do this postulate contains any undefined term ? Is this postulate consistent ? Do they follow from Euclid’s postulate ? Explain.
View SolutionConsider ‘postulate’ given below. There exist at least three points that are not on the same line. Do this postulate contains any undefined term ? Is this postulate consistent ? Do they follow from Euclid’s postulate ? Explain.
View Solution
