Convert the following recurring decimals into rational numbers :
(i) 0.4⋅3⋅7 (ii) 1.7⋅2⋅3
(iii) 0.⋅2⋅3⋅1 (iv) 0.4⋅5⋅6
The correct Answer is:(i) 433990 (ii) 853495 (iii) 77333 (iv)226495
To convert the given recurring decimals into rational numbers, we will follow a systematic approach for each case. Here’s the step-by-step solution for each part of the question:
1. Let x = 0.437373737... (where 37 is repeating)
2. Multiply by 10:
\( 10x = 4.37373737... \)
3. Multiply by 1000:
\( 1000x = 437.37373737... \)
4. Set up the equations:
- Equation 1: \( x = 0.437373737... \)
- Equation 2: \( 1000x = 437.37373737... \)
5. Subtract Equation 1 from Equation 2:
\( 1000x - 10x = 437.37373737... - 4.37373737... \)
\( 990x = 433 \)
6. Solve for x:
\( x = \frac{433}{990} \)
(ii) Convert 1.7˙2˙3 into a rational number.
1. Let y = 1.723232323... (where 23 is repeating)
2. Multiply by 10:
\( 10y = 17.23232323... \)
3. Multiply by 1000:
\( 1000y = 1723.23232323... \)
4. Set up the equations:
- Equation 1: \( y = 1.723232323... \)
- Equation 2: \( 1000y = 1723.23232323... \)
5. Subtract Equation 1 from Equation 2:
\( 1000y - 10y = 1723.23232323... - 17.23232323... \)
\( 990y = 1706 \)
6. Solve for y:
\( y = \frac{1706}{990} \)
Simplifying gives \( y = \frac{853}{495} \).
(iii) Convert 0.0˙2˙3˙1 into a rational number.
1. Let z = 0.023123123... (where 231 is repeating)
2. Multiply by 1000:
\( 1000z = 23.123123123... \)
3. Multiply by 10:
\( 10z = 0.231231231... \)
4. Set up the equations:
- Equation 1: \( z = 0.023123123... \)
- Equation 2: \( 1000z = 23.123123123... \)
5. Subtract Equation 1 from Equation 2:
\( 1000z - 10z = 23.123123123... - 0.231231231... \)
\( 990z = 23 - 0.023 = 23.1 \)
6. Solve for z:
\( z = \frac{23.1}{990} \)
Converting \( 23.1 \) to a fraction gives \( z = \frac{231}{990} \) and simplifying gives \( z = \frac{77}{330} \).
(iv) Convert 0.4˙5˙6 into a rational number.
1. Let p = 0.456565656... (where 56 is repeating)
2. Multiply by 10:
\( 10p = 4.56565656... \)
3. Multiply by 1000:
\( 1000p = 456.56565656... \)
4. Set up the equations:
- Equation 1: \( p = 0.456565656... \)
- Equation 2: \( 1000p = 456.56565656... \)
5. Subtract Equation 1 from Equation 2:
\( 1000p - 10p = 456.56565656... - 4.56565656... \)
\( 990p = 452 \)
6. Solve for p:
\( p = \frac{452}{990} \)
Simplifying gives \( p = \frac{226}{495} \).
Summary of Results:
1. \( 0.4̇3̇7 = \frac{433}{990} \)
2. \( 1.7̇2̇3 = \frac{853}{495} \)
3. \( 0.0̇2̇3̇1 = \frac{77}{330} \)
4. \( 0.4̇5̇6 = \frac{226}{495} \)
2. Multiply by 10:
\( 10x = 4.37373737... \)
3. Multiply by 1000:
\( 1000x = 437.37373737... \)
4. Set up the equations:
- Equation 1: \( x = 0.437373737... \)
- Equation 2: \( 1000x = 437.37373737... \)
5. Subtract Equation 1 from Equation 2:
\( 1000x - 10x = 437.37373737... - 4.37373737... \)
\( 990x = 433 \)
6. Solve for x:
\( x = \frac{433}{990} \)
2. Multiply by 10:
\( 10y = 17.23232323... \)
3. Multiply by 1000:
\( 1000y = 1723.23232323... \)
4. Set up the equations:
- Equation 1: \( y = 1.723232323... \)
- Equation 2: \( 1000y = 1723.23232323... \)
5. Subtract Equation 1 from Equation 2:
\( 1000y - 10y = 1723.23232323... - 17.23232323... \)
\( 990y = 1706 \)
6. Solve for y:
\( y = \frac{1706}{990} \)
Simplifying gives \( y = \frac{853}{495} \).
2. Multiply by 1000:
\( 1000z = 23.123123123... \)
3. Multiply by 10:
\( 10z = 0.231231231... \)
4. Set up the equations:
- Equation 1: \( z = 0.023123123... \)
- Equation 2: \( 1000z = 23.123123123... \)
5. Subtract Equation 1 from Equation 2:
\( 1000z - 10z = 23.123123123... - 0.231231231... \)
\( 990z = 23 - 0.023 = 23.1 \)
6. Solve for z:
\( z = \frac{23.1}{990} \)
Converting \( 23.1 \) to a fraction gives \( z = \frac{231}{990} \) and simplifying gives \( z = \frac{77}{330} \).
2. Multiply by 10:
\( 10p = 4.56565656... \)
3. Multiply by 1000:
\( 1000p = 456.56565656... \)
4. Set up the equations:
- Equation 1: \( p = 0.456565656... \)
- Equation 2: \( 1000p = 456.56565656... \)
5. Subtract Equation 1 from Equation 2:
\( 1000p - 10p = 456.56565656... - 4.56565656... \)
\( 990p = 452 \)
6. Solve for p:
\( p = \frac{452}{990} \)
Simplifying gives \( p = \frac{226}{495} \).
1. \( 0.4̇3̇7 = \frac{433}{990} \)
2. \( 1.7̇2̇3 = \frac{853}{495} \)
3. \( 0.0̇2̇3̇1 = \frac{77}{330} \)
4. \( 0.4̇5̇6 = \frac{226}{495} \)
Topper's Solved these Questions
- SEQUENCE AND SERIESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - SEQUENCE AND SERIESEXERCISE - Exercise 9I
9 Videos
- SEQUENCE AND SERIESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - SEQUENCE AND SERIESEXERCISE - Exercise 9J
16 Videos
- SEQUENCE AND SERIESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - SEQUENCE AND SERIESEXERCISE - Exercise 9G
17 Videos
- RELATIONS AND FUNCTIONSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - RELATIONS AND FUNCTIONSEXERCISE - MISCELLANEOUS EXERCISE
12 Videos
- SETSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - SETSEXERCISE - MISC Exercise
16 Videos
Similar Questions
Knowledge Check
Compound having −O∣∣C−CH3 group reacts rapidly with halogen in presence of a base to form haloform. The reaction is known as haloform.
R−O∣∣C−CH3X2+ϴOH−−−−→R−O∣∣C−ϴO+CHX3
Mechanism
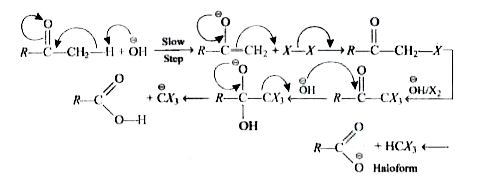
Consider the following reactions:
Reaction I →Ph−O∣∣C−CH3Cl2,ϴOH−−−−→Ph−O∣∣C−ϴO+CHCl3
Reaction II →Ph−O∣∣C−CD3−Cl2,ϴOH−−−−→Ph−O∣∣C−ϴO+CDCl3
Which of the following is correct comparison of the rate of reaction I and II?ArI>rIIBrI>rIICrI=rIIDCannot be determinedConsider the following nucleophiles CF3−O∣∣S∣∣OI−ΘO,Ph−O∣∣S∣∣OII−ΘO,PIII−ΘO,CH3−O∣∣CIV−ΘO when attached to sp3 -hybridized carbon, their leaving group ability in nucleophilic substitution reactions decreases in the order
AI>II>III>IVBI>II>IV>IIICIV>I>II>IIIDIV>III>II>IArrange the following anions in decreasing order of stability :
H−O∣∣C−өCH−O∣∣C−H(P) CH3−O∣∣C−өCH−O∣∣C−H(Q)
CH3−O∣∣C−өCH−O∣∣C−..O..−CH3(R)AR>Q>PBQ>R>PCP>R>QDP>Q>R
The order of stability of the following tautomeric compounds is
(i). CH2=OH∣CH−CH2−O∣∣C−CH3⇔
(ii). CH3−O∣∣C−CH2−O∣∣C−CH3⇔
(iii). CH3−OH∣C=CH−O∣∣C−CH3
View SolutionThe order of stability of the following tautomeric compounds is
(i). CH2=OH∣CH−CH2−O∣∣C−CH3⇔
(ii). CH3−O∣∣C−CH2−O∣∣C−CH3⇔
(iii). CH3−OH∣C=CH−O∣∣C−CH3
View SolutionWrite the IUPAC name of the following compound:
CH3−O∣∣C−CH3∣CH−Cl∣C∣C2H5−CH3∣CH−NO2∣CH−CH∣C2H5−CH3
View SolutionArrange the following compounds in decreasing order of nucleophilic addition reaction
H−O∣∣CI−H H3C−O∣∣CII−H H3C−O∣∣CIII−CH3
View SolutionThe IUPAC name of CH3−CH3∣CH−CH3∣CH−CH2NH2 is
View Solution

