Coplanar points are the points that are in the same plane. Thus, Can 150 points be coplanar? Can 3 points be non-coplanar?
Step-by-Step Solution:
1. Understanding Coplanar Points:
- Coplanar points are defined as points that lie on the same plane. A plane is a flat, two-dimensional surface that extends infinitely in all directions.
2. Analyzing the First Part of the Question:
- The question asks if 150 points can be coplanar.
- Since a plane can contain an infinite number of points, it is possible for 150 points to lie on the same plane.
- Therefore, the answer to the first part is Yes, 150 points can be coplanar.
3. Understanding Non-Coplanar Points:
- Non-coplanar points are points that do not lie on the same plane.
4. Analyzing the Second Part of the Question:
- The question asks if 3 points can be non-coplanar.
- To determine this, we need to recall that any two points always define a line, and any three points will always lie on the same plane unless they are collinear (i.e., all three points lie on the same straight line).
- However, for three points to be considered non-coplanar, they must not all lie on the same plane.
- It is not possible for just three points to be non-coplanar, as they can always be arranged in a way that they lie on the same plane.
- Therefore, the answer to the second part is No, three points cannot be non-coplanar.
Summary of Answers:
- Can 150 points be coplanar? Yes.
- Can 3 points be non-coplanar? No.
- Coplanar points are defined as points that lie on the same plane. A plane is a flat, two-dimensional surface that extends infinitely in all directions.
- The question asks if 150 points can be coplanar.
- Since a plane can contain an infinite number of points, it is possible for 150 points to lie on the same plane.
- Therefore, the answer to the first part is Yes, 150 points can be coplanar.
- Non-coplanar points are points that do not lie on the same plane.
- The question asks if 3 points can be non-coplanar.
- To determine this, we need to recall that any two points always define a line, and any three points will always lie on the same plane unless they are collinear (i.e., all three points lie on the same straight line).
- However, for three points to be considered non-coplanar, they must not all lie on the same plane.
- It is not possible for just three points to be non-coplanar, as they can always be arranged in a way that they lie on the same plane.
- Therefore, the answer to the second part is No, three points cannot be non-coplanar.
- Can 150 points be coplanar? Yes.
- Can 3 points be non-coplanar? No.
Topper's Solved these Questions
Similar Questions
In how many points a line, not in a plane, can intersect the plane?
View SolutionStatement-1: There are p≥8 points in space no four of which are in the same with exception of q≥3 points which are in the same plane, then the number of planes each containing three points is .pC3−.qC3.
Statement-2: 3 non-collinear points alwasy determine unique plane.View Solution
Knowledge Check
- Question 1 - Select One
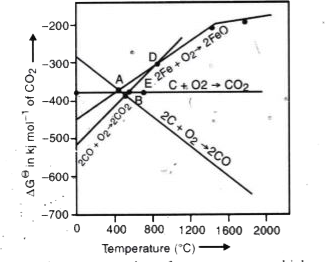
Below point 'A' FeO canAbe reduced by carbon monoxide only.Bbe reduced by both carbon monoxide and carbon.Cbe reduced by carbon only.Dnot be reduced by both carbon and carbon monoxide. - Question 2 - Select One

Below point 'A' FeO canAbe reduced by carbon monoxide only.Bbe reduced by both carbon monoxide and carbon.Cbe reduced by carbon only.Dnot be reduced by both carbon and carbon monoxide. - Question 3 - Select One

Below point 'A' FeO canAbe reduced by carbon monoxide only.Bbe reduced by both carbon monoxide and carbon.Cbe reduced by carbon only.Dnot be reduced by both carbon and carbon monoxide.
Mark the following points on a sheet of paper. Tell how many line segments can be obtained in each case: Two points A, B. Three non-collinear points A, B, C. Four points such that no three of them belong to the same line. Any five points so that on three of them are collinear.
View SolutionIn how many points two distinct planes can intersect?
View SolutionThere are 16 points in a plane of which 6 points are collinear and no other 3 points are collinear.Then the number of quadrilaterals that can be formed by joining these points is
View SolutionThere are n points in a plane of which 'p' points are collinear. How many lines can be formed from these points
View SolutionA point has polar coordinate (2,60∘) The same point can be represented by
View Solution

