(Cosine Formulae) if $a, b, c$ are the lengths of the sides opposite respectively to the angles $A, B, C$ of a triangle $A B C,$ show that (I) $cos A = \frac{b^{2} + c^{2} - a^{2}}{2 b c}$ (ii) $cos B = \frac{c^{2} + a^{2} - b^{2}}{2 a c}$ (iii) (i) $cos C = \frac{a^{2} + b^{2} - c^{2}}{2 a b}$

Video Solution

Text Solution

Verified by Experts

Here, components of C are c cos A and c sin A is drawn.

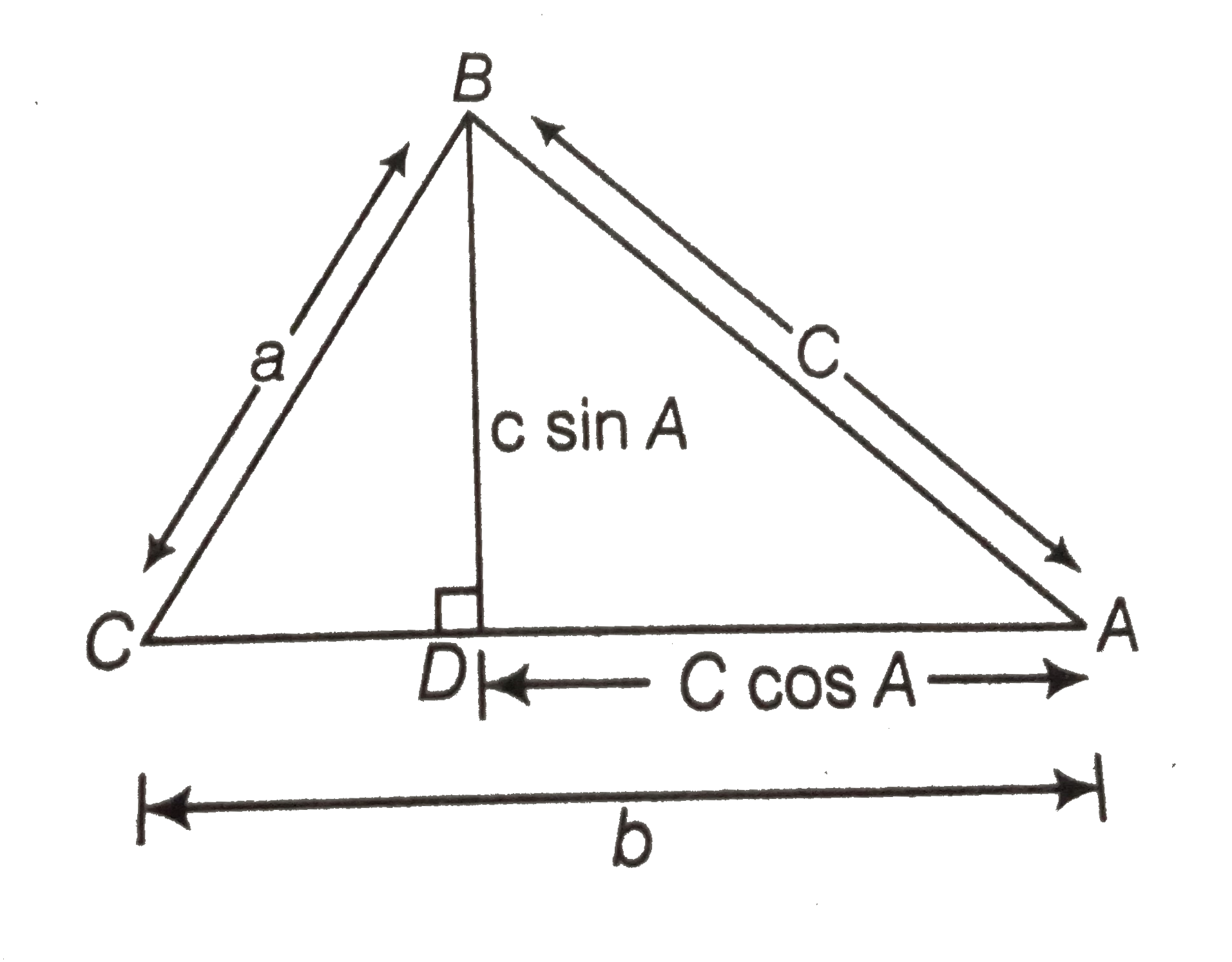
Since, $- - \to C D = b - c cos A$
In $Δ B D S a^{2} = {(b - cos A)}^{2} + {(c sin A)}^{2}$
$\Rightarrow a^{2} = b^{2} + c^{2} {cos}^{2} A - 2 b c cos A + c^{2} {sin}^{2} A$
$\Rightarrow 2 b c cos A = b^{2} - a^{2} + c^{2} ({cos}^{2} A {sin}^{2} A)$
$∴ cos A = \frac{b^{2} + c^{2} - a^{2}}{2 a b}$

Updated on:21/07/2023

|

Class 12 MATHS VECTOR ALGEBRA

Topper's Solved these Questions

Similar Questions

NCERT EXEMPLAR ENGLISH-VECTOR ALGEBRA-LONG ANSWER TYPE QUESTIONS

Home
Ask Doubt
Profile