D,E and F are respectively the mid-points of the sides BC, CA and AB of △ABC show that
(i) BDEF is a parallelogram.
(ii) ar (DEF) = 14 ar (ABC)
(iii) ar(BDEF)=12 ar (ABC) Solution in Kannada
The correct Answer is:(i) BDE F is a parallelogram
(ii) 14
12
Step by step video, text & image solution for D,E and F are respectively the mid-points of the sides BC, CA and AB of triangle ABC show that (i) BDEF is a parallelogram. (ii) ar (DEF) = 1/4 ar (ABC) (iii) ar (BDEF) = 1/2 ar (ABC) by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- AREAS OF PARALLELOGRAMS AND TRIANGLESBOOK - CPC CAMBRIDGE PUBLICATIONCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Exercise 11.4
8 Videos
- AREAS OF PARALLELOGRAMS AND TRIANGLESBOOK - CPC CAMBRIDGE PUBLICATIONCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLESEXERCISE - EXERCISE 11.2
6 Videos
- CIRCLES BOOK - CPC CAMBRIDGE PUBLICATIONCHAPTER - CIRCLES EXERCISE - EXERCISE 12.6
4 Videos
Similar Questions
Parallelogram ABCD and rectangle ABEF are on the base AB and have equal areas. Show that the perimeter of the parallelogram is greater than that of the rectangle.
View SolutionIn the given figure, ABCD is a parallelogram , AE⊥DCandCF⊥AD . If AB = 16 cm, AE = 8 cm and CF = 10 cm, find AD.
View SolutionProve that the line of centres of two intersecting circles subtends equal angles at the two point of intersection.
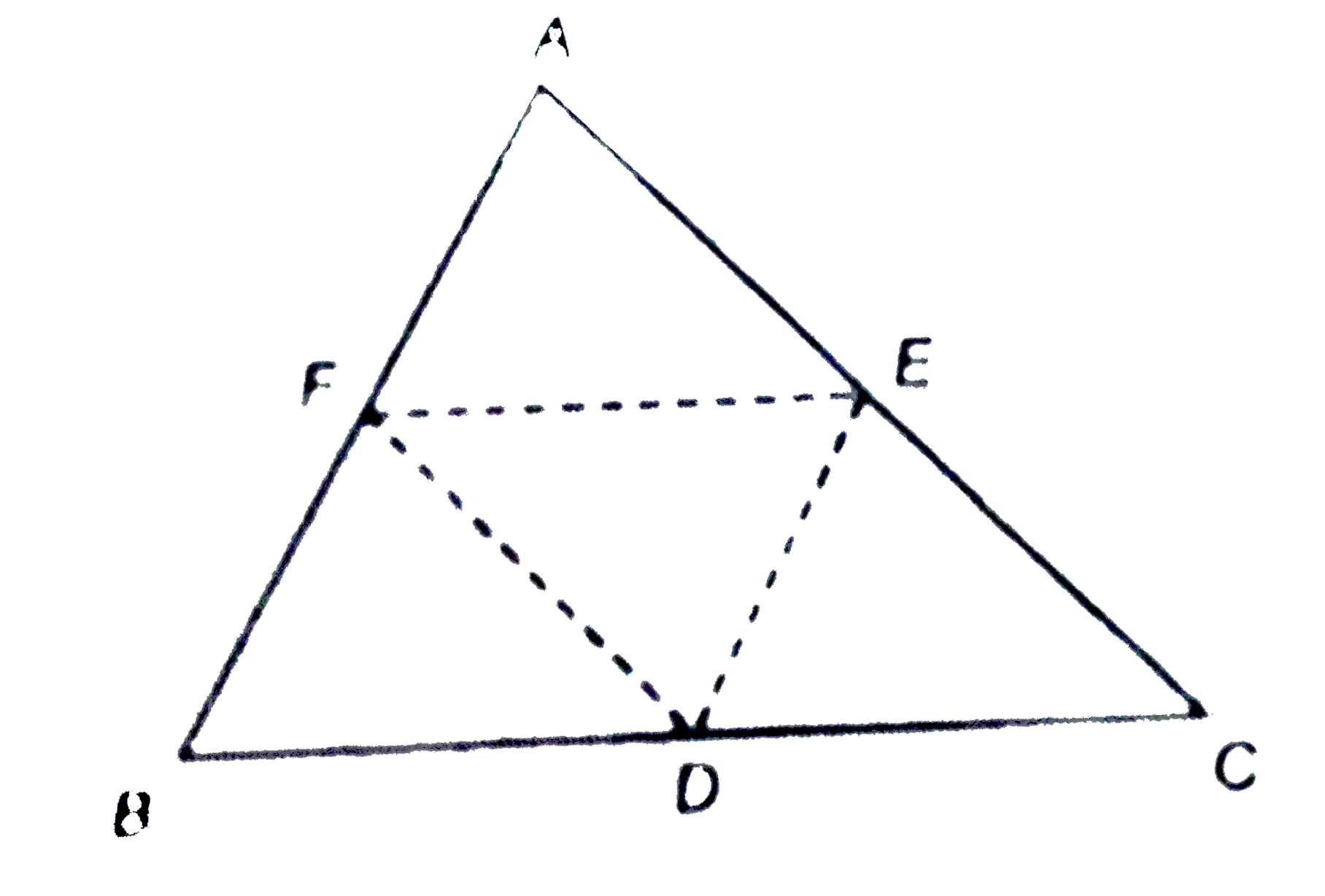
View SolutionIn the adjoining figure D, E and F are the mid-points of the sides BC, CA and AB respectively of ΔABC. Prove that:
(i) □BDEF is a parallelogram
(ii) area of ΔDEF=14× area of ΔABC
(iii) area of □BDEF=12× area of ΔABC
View SolutionD, E, F are the midpoints of the sides BC, CA and AB respectively of △ABC. Prove that
(i) BDEF is a ||gm,
(ii) ar(△DEF)=14ar(△ABC)and
(iii) ar(||gm BDEF)=12ar(△ABC)
View Solutionत्रिभुज ABC की भुजाओं BC , CA तथा AB के मध्य-बिंदु क्रमशा D , E तथा F है। सिद्ध कीजिए कि BDEF एक समांतर चतुर्भुज है जिसका क्षेत्रफल ΔABC का आधा है। साथ ही, सिद्ध कीजिए कि ar(ΔDEF)=14ar(ΔABC) तथा ar(।।gmBDEF)=12ar(ΔABC)
View SolutionD, E और F क्रमशः त्रिभुज ABC की भुजाओं BC, CA और AB के मध्य-बिन्दु है। दर्शाइए कि :
(i) BDEF का समान्तर चतुर्भुज है।
(ii) ar(DEF)=14ar(ABC)
(iii) ar(BDEF)=12ar(ABC)
View SolutionD, E तथा F, ΔABC कि क्रमश : भुजाओ BC, CA तथा AB के मध्यबिंदु है। सिद्ध कीजिए कि BDEF एक समांतर चतुर्भुज है तथा इसका क्षेत्रफल ΔABC के क्षेत्रफल का आधा है।
यह भी दिखाइए कि ar(DEF)=14ar(ABC).
View SolutionP and Q are respectively the mid-points of sides AB and BC of a triangle ABC and R is the mid point at AP, show that
(i) ar (PQR) = 12 ar (ARC)
(ii) ar (RQC) = 38 ar (ABC)
(iii) ar (PBQ) = ar (ARC)
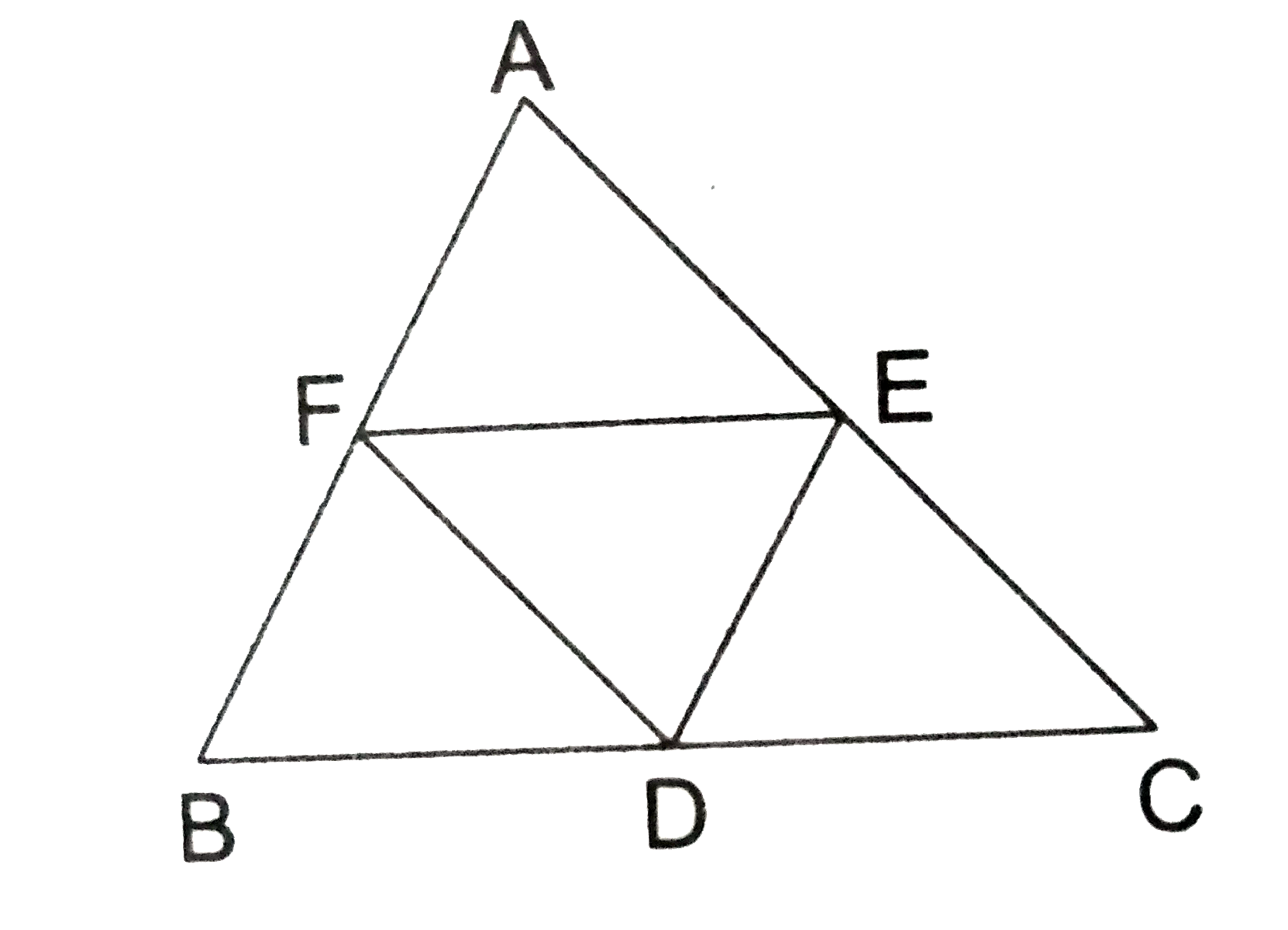
View SolutionIn the figure, ΔABC, D, E, F are the midpoints of sides BC, CA and AB respectively. Show that
(i) BDEF is a parallelogram
(ii) ar(ΔDEF)=14ar(ΔABC)
(iii) ar(BDEF)=12ar(ΔABC)
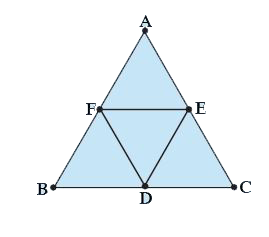
View SolutionIn the figure, ΔABC, D, E, F are the midpoints of sides BC, CA and AB respectively. Show that
(i) BDEF is a parallelogram
(ii) ar(ΔDEF)=14ar(ΔABC)
(iii) ar(BDEF)=12ar(ΔABC)
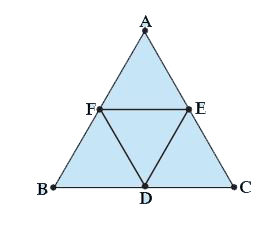
View SolutionIn the figure, ΔABC, D, E, F are the midpoints of sides BC, CA and AB respectively. Show that
(i) BDEF is a parallelogram
(ii) ar(ΔDEF)=14ar(ΔABC)
(iii) ar(BDEF)=12ar(ΔABC)
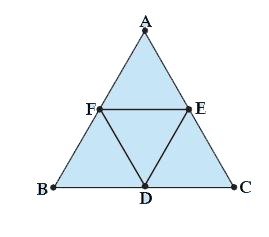
View SolutionD, E and F are the midpoints of triangles ABC BC, CA and AB respectively. ar (DEF) =1/4 ar (ABC)
View SolutionD, E ਅਤੇ F ਕ੍ਰਮਵਾਰ ਤ੍ਰਿਭੁਜ ABC ਦੀਆਂ ਭੁਜਾਵਾਂ BC,CA ਅਤੇ AB ਦੇ ਮੱਧ-ਬਿੰਦੂ ਹਨ।ਦਰਸਾਉ ਕਿ:- ar(BDEF)=12ar(ABC)
View SolutionD, E and F are the mid-points of the sides BC, CA and AB respectively of triangle ABC. Prove that:
BDEF is a parallelogram.
View Solution
