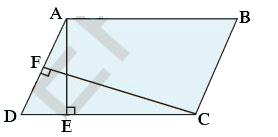
DE is the perpendicular drawn from D of the parallelogram ABCD to its side AB and BF is the perpendicular drawn from B of ABCD to its side AD. If AB = 10cm, AD = 8 cm and DE = 6 cm, then find BF. Solution in Bengali
To solve the problem, we need to find the length of BF in the parallelogram ABCD. Given that DE and BF are perpendicular heights from vertices D and B to sides AB and AD respectively, we can use the area of the parallelogram to find BF.
1. Understand the problem:
- AB=10 cm
- AD=8 cm
- DE=6 cm
- We need to find BF.
2. Calculate the area of the parallelogram using DE and AB:
- The area of the parallelogram can be calculated using the base AB and height DE.
- Area = Base × Height = AB×DE
- Area = 10 cm × 6 cm = 60 cm²
3. Express the area of the parallelogram using BF and AD:
- The area of the parallelogram can also be calculated using the base AD and height BF.
- Area = Base × Height = AD×BF
- Area = 8 cm × BF
4. Set the two expressions for the area equal to each other:
- Since both expressions represent the area of the same parallelogram, they must be equal.
- 10×6=8×BF
- 60=8×BF
5. Solve for BF:
- Divide both sides of the equation by 8 to isolate BF.
- BF=608
- BF=7.5 cm
Final Answer:
BF=7.5 cm
- AB=10 cm
- AD=8 cm
- DE=6 cm
- We need to find BF.
- The area of the parallelogram can be calculated using the base AB and height DE.
- Area = Base × Height = AB×DE
- Area = 10 cm × 6 cm = 60 cm²
- The area of the parallelogram can also be calculated using the base AD and height BF.
- Area = Base × Height = AD×BF
- Area = 8 cm × BF
- Since both expressions represent the area of the same parallelogram, they must be equal.
- 10×6=8×BF
- 60=8×BF
- Divide both sides of the equation by 8 to isolate BF.
- BF=608
- BF=7.5 cm
BF=7.5 cm
Topper's Solved these Questions
- THEOREMS ON AREASBOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS ON AREASEXERCISE - EXERCISE-3
40 Videos
- SET THEORYBOOK - CALCUTTA BOOK HOUSECHAPTER - SET THEORYEXERCISE - EXERCISE-1
37 Videos
- THEOREMS ON CONCURRENCEBOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS ON CONCURRENCEEXERCISE - EXERCISE Long-answer type questions
17 Videos
Similar Questions
D is any point on the side QR of the parallelogram PQRS. ΔPQDandΔSDR have the areas 16 sq.cm and 20 sq.cm respectively, then QD : RD =
View SolutionState which of the following are sets and which are not:
A=A group of students of class-IX having heights from 4ft to 5ft,
View SolutionFind the value of k for which the given value is a solution of the given equation 7x2+kx−3=0 at x=23
View SolutionABCD is a Parallelogram. AE is perpendicular on DC and CF is perpendicular on AD. If AB= 10cm, AE = 8cm, CF =12cm . Find AD ?
View SolutionAssertion (A) : In the given figlure, ABCD is a ||gm in which DE⊥ADandBF⊥AD. If AB = 16 cm, DE = 8 cm and BF = 10 cm then what is the length of AD?.
View Solutionसमांतर चतुर्भुज ABCD में, AB=10 सेमी है। यदि भुजाओं AB तथा AD की संगत ऊँचाइयां क्रमशः 7 सेमी तथा 8 सेमी है, तो AD का मान ज्ञात कीजिए।
View SolutionLet ABCD be a quadrilateral with area 18, with side AB parallel to the side CD and AB = 2 CD. Let AD be perpendicular to AB and CD. If a circle is drawn inside the quadrilateral ABCD touching all the sides, then its radius is :
View SolutionABCD is a parallelogram. AE is perpendicular on DC and CF is perpendicular on AD. If AB = 10 cm, AE = 8 cm and CF = 12 cm. Find AD.
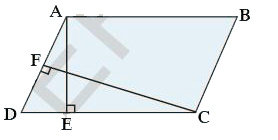
View SolutionABCD is a parallelogram. AE is perpendicular on DC and CF is perpendicular on AD. If AB = 10 cm, AE = 8 cm and CF = 12 cm. Find AD.
View Solutionमाना ABCD एक चतुर्भुज है जिसका क्षेत्रफल 18 वर्ग इकाई है। चतुर्भुज में भुजा AB, CD के समान्तर है तथा AB = 2CDl माना AB व CD के लम्बवत AD है। यदि चतुर्भुज ABCD के अन्दर चारों भुजाओं को स्पर्श करता हुआ एक वृत्त खींचा जाता है, तब उसकी त्रिज्या है
View Solutionमाना ABCD एक चतुर्भुज है जिसका क्षेत्रफल 18 है। भुजा AB भुजा CD के समान्तर है तथा AB = 2CD. माना AD, AB और CD के लम्बवत् है। यदि एक वृत्त, चतुभुज ABCD के अन्दर, सभी भुजाओं को स्पर्श करता हुआ खींचा जाए, तब इसकी त्रिज्या है
View SolutionIn ∣∣gm ABCD, AB = 14 cm. The altitude corresponding to sides AB and AD are 8 cm and 7 cm. Find AD.
View SolutionLet ABCD be a quadrilateral with area 18. with side AB parallel to the side CD and CD = 2 AB. Let AD be perpendicular to AB and CD. If a circle is drawn inside the quadrilateral ABCD touching all the sides, then its radius is
View SolutionThe cost price of an article is Rs 7840. What should be the selling price of the article so that there is a profit of 7 % ?
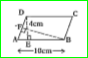
View SolutionIn parallelogram ABCD, AB= 10cm DE=4cm. find i) the area of ABCD. ii) the length of BF, if AD =6cm
.
View Solution
