Define a function f : R → R by
f(x)=max{|x|,|x−1|,...|x−n|}
where n is a fixed natural number. Then 2nf0f(x)dx is -
A
n
B
n2
C
3n
D
3n2
Video Solution
Text Solution
The correct Answer is:D
f(x)=max{|x|,|x−1|,...|x−n|}
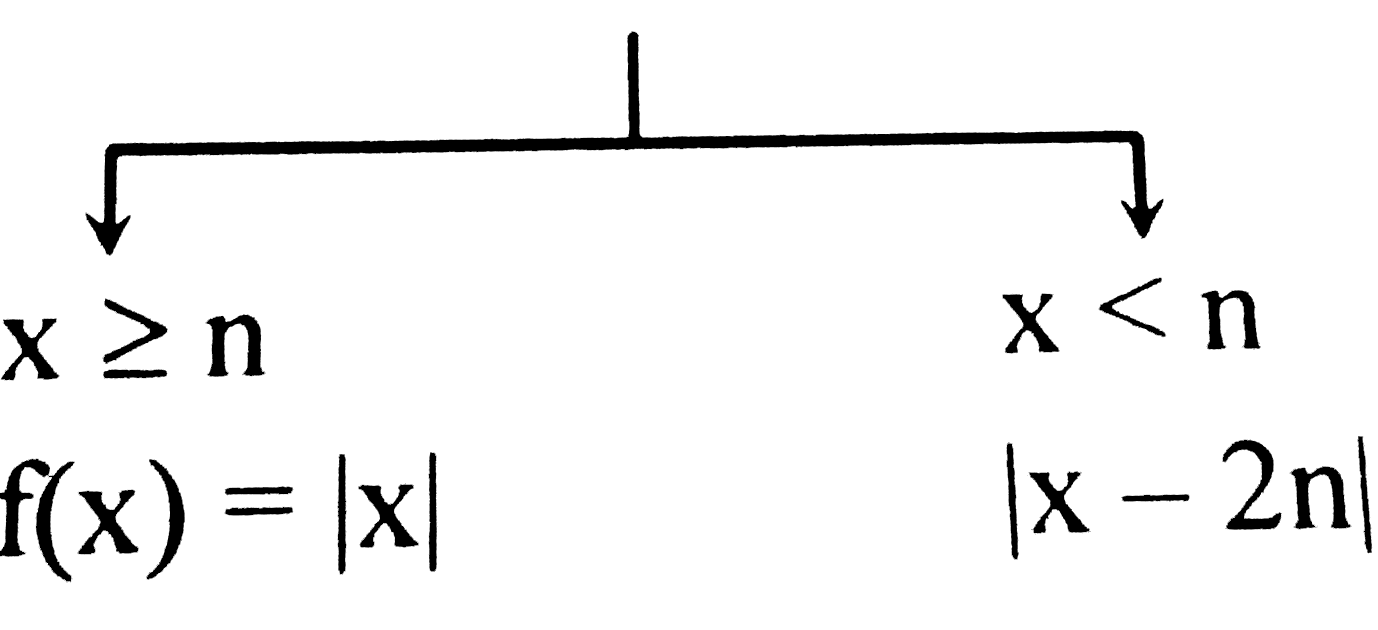
∫2n0f(x)dx=∫n0f(x)dx+∫2nnf(x)dx
=∫n0|x−2n|dx+∫2nn|x|dx
=∫n0(2n−x)dx+∫2nnx.dx
=[2nx−x22]n0+[x22]2nn
(2n2−n22)+(4n22−n22)
=3n22+3n22=3n22nf0f(x)dx=nf0f(x)dx+2nf0f(x)dx
=nf0|x−2n|dx+2nf0|x|dx
=nf0(2n−x)dx+2nf0x.dx
|
Similar Questions
Knowledge Check
Let function f:R→R be defined by f (x) = 2x + sin x for x ∈ R Then f is
Aone-to-one and ontoBone-to-one but NOT ontoConto but NOT one-to-oneDneither one-to-one nor ontoLet f:N→N be defined by
f(x)=x−(1)x∀x∈N, Then f isAone-to-one but not ontoBone-to-one and ontoConto but not one-to-oneDneither onto nor one-to-oneLet f:R→R be a function defined by f(x)=x−mx−n, where m≠n. Then
Af is one-one ontoBf os one-one intoCf is many-one ontoDf is many-one into
Let a function f:R→R be defined by f(x)=2x+cosx+sinx for x∈R. Then find the nature of f(x).
View Solutionlet f:R→R be a function defined by f(x)=max{x,x3}. The set of values where f(x) is differentiable is:
View SolutionSuppose that a function f:R→R satisfies f(x+y)=f(x)f(y) for all x y∈R and f(1)=3 . If n∑i=lf(i)=363, then n is equa to _______ .
View SolutionIf f(x) is a polynomial of degree n(>2) and f(x)=f(α−x),
(where α is a fixed real number ), then the degree of f'(x) is
View SolutionThe function f:N→N,N being the set of of natural numbers, defined by f(x)=2x+3 is
View Solution
