Define limit what it represents
Video Solution
|
Answer
Step by step video & image solution for Define limit what it represents by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Similar Questions
Knowledge Check
Recognise the figure and find out the correct matching
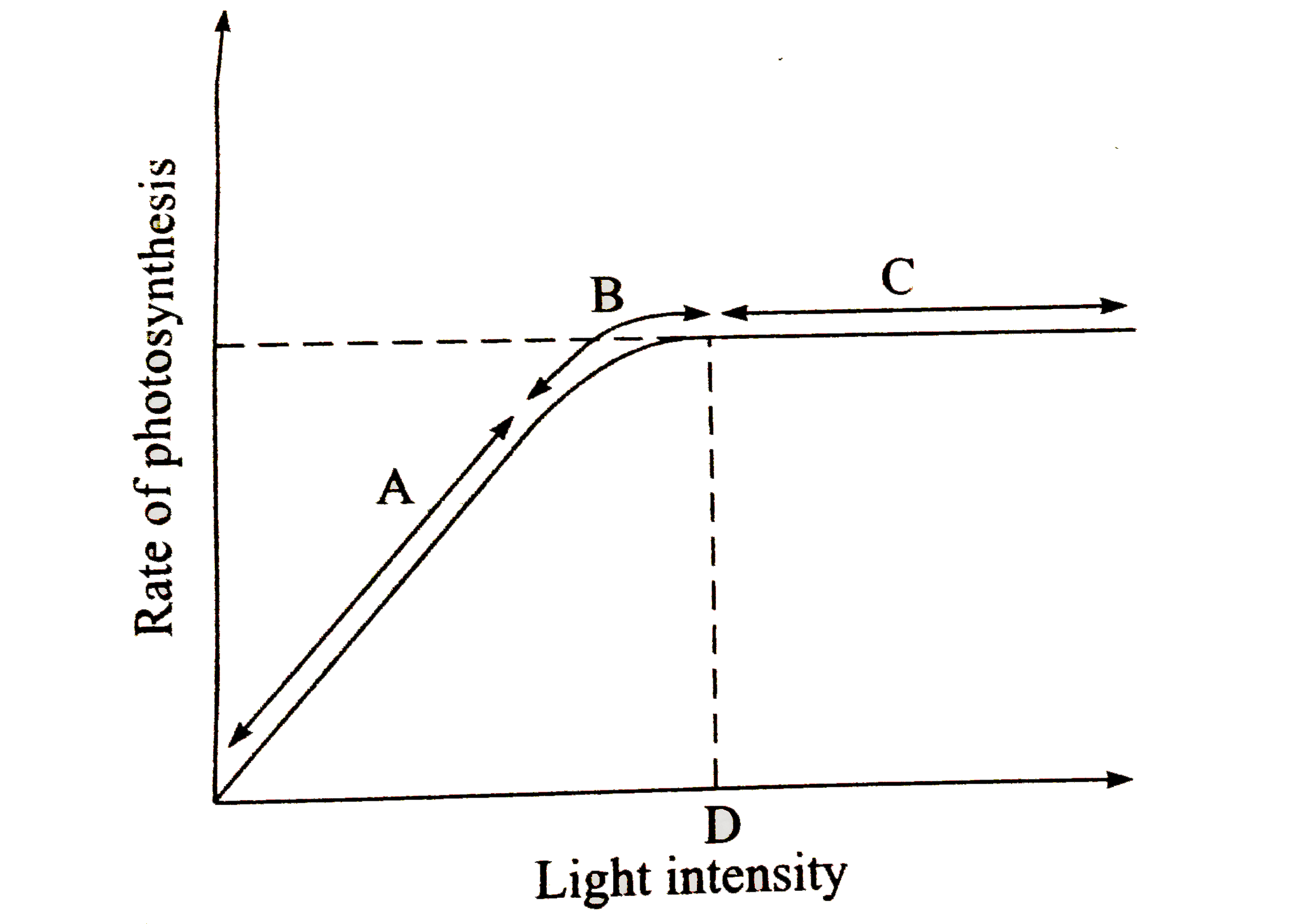
a. At which point in the curve light is a limiting factor?
b. What do 'C' represent on the curve?
c. What do 'D' represent on the curve?
d. What do 'E' represent on the curve?Aa- A, b-light saturation point, c-maximum rate of photosynthesis, d- factors other than light become limitingBa-B, b-maximum rate of photosynthesis, c- light saturation point, d-factors other than light become limitingCa- A, b-factors other than light become limiting, c-light saturation point, d-maximum rate of photosynthesisDa-A, b-factors other than light become limiting, c-maximum rate of photosynthesis, d-light saturation pointLimiting molar conductivity of an electrolyte can be represented as the sum of the individual contributions of anions and cations. This law was given by
AFaradayBOstwaldCDavyDKohlrausch
Define energy level. How is it represented?
View SolutionDefine Boyle's law. How is it represented mathematically ?
View Solutionwhat is the investment limit in equipment for micro serive enterprises ?
View SolutionWhat is the investment limit in equipment for micro service enterprises ?
View SolutionDefine limiting molar conductivity. Why does conductivity of an electrolyte decrease with discrease in concentration.
View SolutionDefine limiting molar conductivity. Why does conductivity of an electrolyte decrease with discrease in concentration.
View Solution
