Define modulus function . Write its domain and range . Draw the graph of it .
Step-by-Step Solution
1. Definition of Modulus Function:
The modulus function, denoted as f(x)=|x|, is defined as follows:
f(x)={xif x≥0−xif x<0
This means that the function returns the absolute value of x, which is always non-negative.
2. Domain of the Modulus Function:
The domain of a function is the set of all possible input values (x-values) for which the function is defined. For the modulus function:
Domain=(−∞,∞)
This indicates that the function is defined for all real numbers.
3. Range of the Modulus Function:
The range of a function is the set of all possible output values (y-values). For the modulus function:
Range=(0,∞)
This means that the output of the function is always non-negative, starting from 0 and going to positive infinity.
4. Graph of the Modulus Function:
To draw the graph of the modulus function f(x)=|x|:
- Plot the points for x≥0: For these values, f(x)=x, which is a straight line passing through the origin with a slope of 1.
- Plot the points for x<0: For these values, f(x)=−x, which is also a straight line passing through the origin but with a slope of -1.
- The graph will be symmetric about the y-axis, as the values for negative x will mirror those for positive x.
The graph will look like a "V" shape, where the vertex is at the origin (0,0).
The modulus function, denoted as f(x)=|x|, is defined as follows:
f(x)={xif x≥0−xif x<0
This means that the function returns the absolute value of x, which is always non-negative.
The domain of a function is the set of all possible input values (x-values) for which the function is defined. For the modulus function:
Domain=(−∞,∞)
This indicates that the function is defined for all real numbers.
The range of a function is the set of all possible output values (y-values). For the modulus function:
Range=(0,∞)
This means that the output of the function is always non-negative, starting from 0 and going to positive infinity.
To draw the graph of the modulus function f(x)=|x|:
- Plot the points for x≥0: For these values, f(x)=x, which is a straight line passing through the origin with a slope of 1.
- Plot the points for x<0: For these values, f(x)=−x, which is also a straight line passing through the origin but with a slope of -1.
- The graph will be symmetric about the y-axis, as the values for negative x will mirror those for positive x.
Topper's Solved these Questions
- MODEL TEST PAPER-6BOOK - ICSECHAPTER - MODEL TEST PAPER-6EXERCISE - SECTION-B
10 Videos
- MODEL TEST PAPER-6BOOK - ICSECHAPTER - MODEL TEST PAPER-6EXERCISE - SECTION - C
10 Videos
- MODEL TEST PAPER-2BOOK - ICSECHAPTER - MODEL TEST PAPER-2EXERCISE - Section-C
10 Videos
- MODEL TEST PAPER-7BOOK - ICSECHAPTER - MODEL TEST PAPER-7EXERCISE - SECTION - C
10 Videos
Similar Questions
Define greatest integer function. Write its domain and range.
View SolutionDefine the function f : R →R by y = f(x) = x2, x∈R. Complete the Table given below by using this definition. What is the domain and range of this function?Draw the graph of f.
View SolutionDefine the function f:R→R by y=f(x)=x4,x∈R. What is the domain and range of this function. Draw the graph of f.
View SolutionDefine the function f:R→R by y=f(x)=x5,x∈R. What is the domain and range of this function. Draw the graph of f.
View SolutionIn the given function, find the co-domain and range
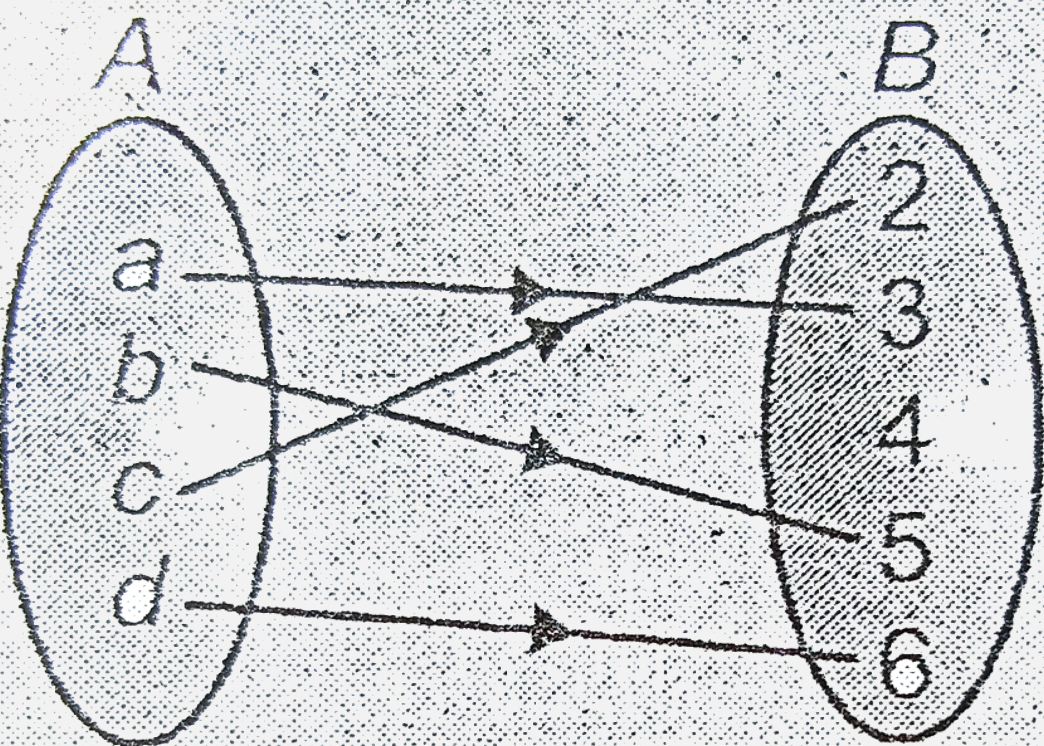
View SolutionDoes the relation {(x,y)|y=|x∣,x∈R} define a function? Write the range and draw the graph.
View SolutionWrite the domain and range of the function f(x)=x−22−x .
View SolutionIn the given function, find the domain, co-domain and range.

View SolutionThe functions defined have domain R

View SolutionThe function f is defined by f(x)=⎧⎪⎨⎪⎩1−x x<01 x=0x+1 x>0⎫⎪⎬⎪⎭. Draw the graph of f(x).
View Solution
