Definition of circle
Circle
In this lesson, you will learn about the area of a circle. Here, we will have a broad explanation about its surface area and also its circumference. We will also look at some solved examples to make it easy for you to understand the concept well.
Definition of Area of Circle
The region which is occupied by the circle in a 2-dimensional plane is called the area of a circle. The formula for the area of the circle is, A=πr2. Here, ‘r’ is the radius of the circle. The area formula is used to measure the space covered by a circular field.
For example, if you are not able to make out as to how much fencing is required for your land plot, then the area formula can be of much help. Another way of explaining is suppose you need to buy a table cloth. It would be possible to know how many portions of cloth you need to buy to cover it completely. In order to figure out such scenarios, the concept of the perimeter and area has been introduced in Maths.
Students might have a doubt as to whether a circle has a volume? Well, the right answer is, “No.” The reason is the fact that a circle is a two-dimensional shape. It has got only perimeter and area. Therefore volume is not present in a circle.
Area of a Circle Formula
Consider a circle with radius r.
You can find a circle above where radius ‘r’ from the centre ‘o’ to the boundary of the circle. In this case, it is to be remembered that the area for this circle A is equal to the product of pi and square of the radius.
Area of a Circle, A = πr2 square units (here ‘r’ is the radius while the value of π = 22/7 or 3.14
Derivation of Area of Circle
When it comes to the area of the circle, it can both visualized as well as proved by using two methods:
- Determining the circle’s area using rectangles
- Determining the circle’s area using triangles
We will now try to have a good understanding of both the methods as below:
Using Areas of Rectangles

There are 16 sectors that are equal in the circle, as shown in the figure above. Here the parallelogram-shaped figure which has been formed by the sectors cut out will be equal to the area of the circle. There will be an equal arc length for each sector since the sectors have equal area. Here, half of the circumference will be contributed by the red colour. In contrast, the other half will be contributed by the blue colour. If there is an increase in the number of sectors cut from the sector, then the shape of the parallelogram would look like a rectangle where breadth will be equal to r and length will be equal to πr.
The area of a rectangle (A) will also be the area of a circle. So, we have
A = πr×r
A = πr2
Using Areas of Triangles
In order to understand this, you need to fill the circle with radius ‘r’ with concentric circles. Look at the figure below where the circle has been cut along the indicated line. Here, the result will be a triangle. The height of the triangle will be equal to the radius of the circle while the base of the triangle would be equal to the circumference of the circle.
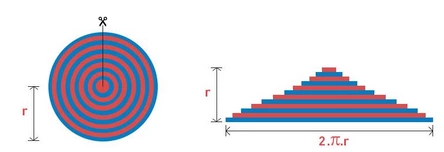
Therefore we find that the area of the triangle (A) will be equal to the area of the circle. We have
A = ½ × base ×height
A = ½ × (2πr) × r
A = πr2
Circle Theorem :
- A tangent to a circle is perpendicular to the radius through the point of contact
- A line drawn through the end point of a radius and perpendicular to it is a tangent to the circle
- The length of two tangents drawn from an external point to a circle are equal
- If two tangents are drawn to a circle from an external point ; then (i) they subtend equal angles at the centre. (ii) they are equally inclined to the line segments ; joining the centre to that point
Surface Area of Circle Formula
A circle is a 2 D representation of a sphere. The surface area of the circle denotes the total area that is taken inside the circle boundary. So, if someone says that the area of the circle is needed then it implies the surface area of the circle itself. In some cases, the area of a circle is also defined by the volume of a circle. It is possible to use the surface formula to find out the surface area provided the length of the diameter or radius is given.
The surface area of the circle = A = π x r2
Circumference of Circle
The length of the boundary defines a perimeter of closed figures. The term, ‘perimeter’ gets changed when it comes to circles. It is known as the circumference of the circle. So, this is the length of the boundary of the circle. When we get a straight line by opening the circle, then the length is known as the circumference. It is required to know the term, ‘pi’ to define the circumference of the circle. Consider the circle as shown below with radius ‘r’ and centre ‘o.’ On the right-hand side, you can see a rope.

The length of the boundary is equal to the perimeter of the circle. It can be measured by using the formula:
Circumference/Perimeter = 2 πr units (here, r is the radius of the circle and π is the pie)
So, here, if we consider the circle with circumference ‘C’ and radius ‘r’, then we get
- π = Diameter/Circumference
- π =C/2r
- C = 2πr
We will now follow some examples where you would be able to get a clear idea of how to apply the different formulas. This would help to clear your concept on the perimeter and circle.
Solved Examples on Area and Circumference of Circle
Question 1:
If the area of a circle is equal to the area of a square. Find out the radius of the circle. ( Square area = 314.159 sq cm)
Solution:
By the formula of the surface area of the circle, we know;
A = π x r2
Now, substituting the value:
314.159 = π x r2
314.159 = 3.14 x r2
r2 = 314.159/3.14
r2 = 100.05
r = √100.05
r = 10 cm
Therefore, the radius of the square is 10 cm
Question 2
Determine the area of a circle, if the circumference of a circle is 30 cm.
Solution:
Given, circumference of a circle = 30 cm
We will now apply the formula of circumference, i.e. C =2 πr
So, we can write,
2πr = 30
or r = 30/2π = 15/π
We have now found the value of r. So, now we can find the area;
A = πr2
A = π (15/ π)2
On solving we get,
A = 71.65 sq.cm.
So, the area of the circumference is 71.65 sq.cm.
Important Chapters:




Similar Questions
Definitions
View SolutionDefinitions
View SolutionDefinitions
View SolutionIntroduction , definition OF circle and locus, equation OF circle, terms related to circle like as chord, reagent, sector, arc etc. area OF sector and segment, orientation OF circle wrt to line- no point common,1 point common and 2 point common
View SolutionOut of the given definitions, which is the most appropriate definition of climate?
View SolutionDefinition Of Shm
View SolutionDefinition of probability
View SolutionDefinition of Numeral
View SolutionDefinition || calculation
View SolutionDefinition Of Surface Tension
View Solution
