ΔI1I2I3 is an excentral triangle of an equilateral triangle ΔABC such that I1I2=4 unit, if ΔDEF is pedal triangle of ΔABC, then Ar(ΔI1I2I3)Ar(ΔDEF)=
16
4
2
1
The correct Answer is:A
Step by step video solution for Delta I_(1)I_(2)I_(3) is an excentral triangle of an equilateral triangle Delta ABC such that I_(1)I_(2)=4 unit, if DeltaDEF is pedal triangle of DeltaABC, then (Ar(Delta I_(1)I_(2)I_(3)))/(Ar (DeltaDEF))= by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SOLUTION OF TRIANGLESBOOK - VK JAISWAL ENGLISHCHAPTER - SOLUTION OF TRIANGLESEXERCISE - Exercise-2 : One or More than One Answer is/are Correct
14 Videos
- SOLUTION OF TRIANGLESBOOK - VK JAISWAL ENGLISHCHAPTER - SOLUTION OF TRIANGLESEXERCISE - Exercise-3 : Comprehension Type Problems
12 Videos
- SEQUENCE AND SERIES BOOK - VK JAISWAL ENGLISHCHAPTER - SEQUENCE AND SERIES EXERCISE - EXERCISE (SUBJECTIVE TYPE PROBLEMS)
21 Videos
- STRAIGHT LINES BOOK - VK JAISWAL ENGLISHCHAPTER - STRAIGHT LINES EXERCISE - Exercise-5 : Subjective Type Problems
10 Videos
Similar Questions
Knowledge Check
A current of 6 A enters one corner P of an equilateral triangle PQR having 3 wires of resistances 2 Q each and leaves by the corner R. Then the currents I1andI2 are
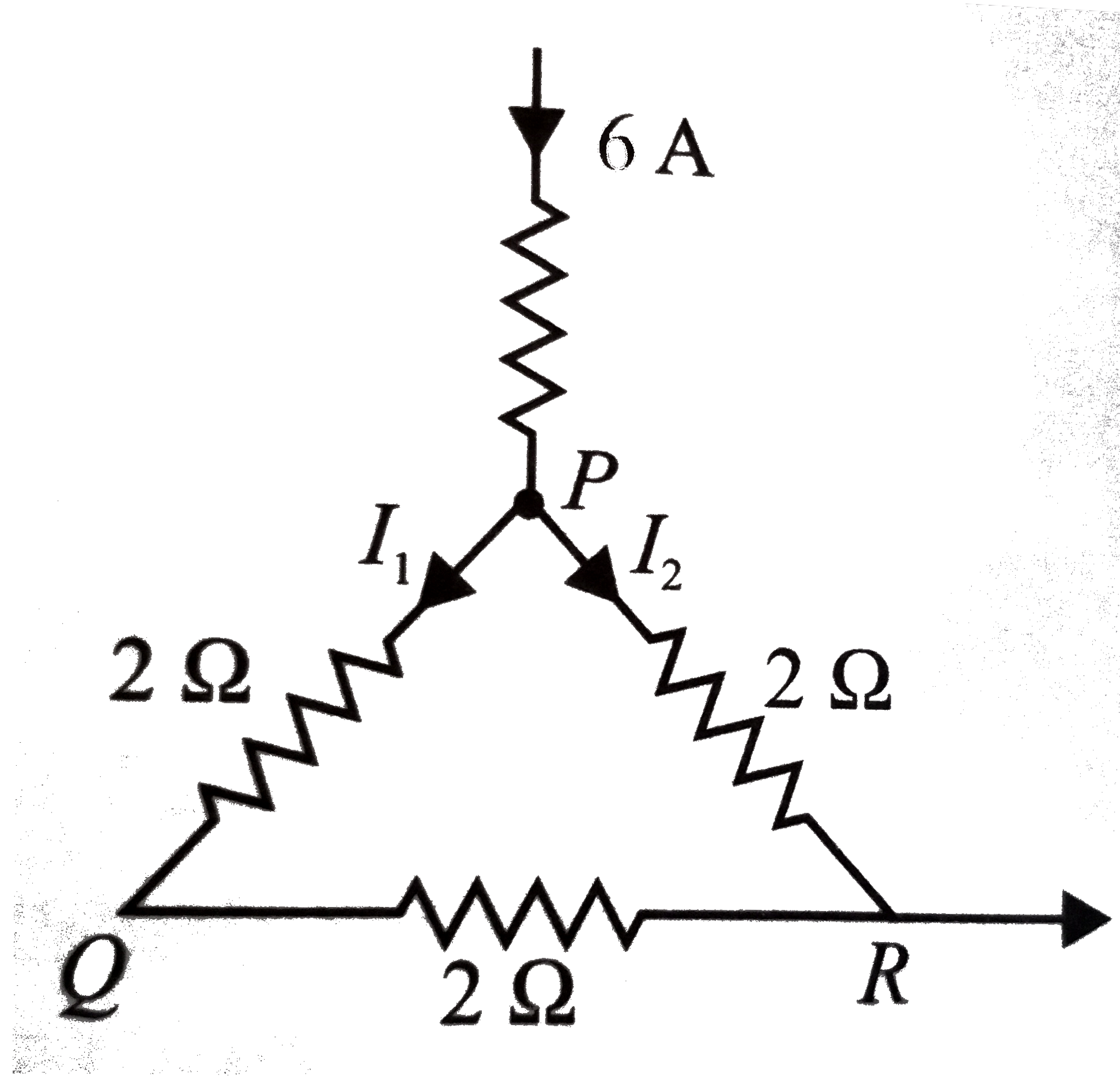 A2A,4AB4A,2AC1A,2AD2A,3A
A2A,4AB4A,2AC1A,2AD2A,3A
If z1,z2andz3, are the vertices of an equilateral triangle ABC such that |z1−i|=|z2−i|=|z3−i|.then |z1+z2+z3|equals:
View SolutionABC and BDE are two equilateral triangles such that D is the mid-point of BC. Then, ar(ΔBDE)=14ar(ΔABC).
View Solutionz1,z2,z3 are the vertices of an equilateral triangle taken in counter clockwise direction. If its circumference is at the origin and z1=1+i, then
View SolutionIn a triangle ABC I1,I2,I3 are excentre of triangle then show that II1.II2.II3=16R2r.
View SolutionIf I1,I2,I3 are excentres of the triangle with vertices (0, 0), (5, 12), (16, 12) then the orthocentre of ΔI1I2I3 is
View SolutionIf I1,I2,I3 are the centers of escribed circles of triangle ABC, show that area of triangle I1I2I3=abc2r.
View Solutionz1,z2,z3 are the vertices of an equilateral triangle taken in counter clockwise direction. If its circumcenter is at (1−2i) and (z1=2+i), then z2=
View Solution
