Determine all the values of $α$ for which the point $(α, α^{2})$ lies inside the triangle formed by the lines. $2 x + 3 y - 1 = 0$ $x + 2 y - 3 = 0$ $5 x - 6 y - 1 = 0$

Video Solution

Text Solution

Verified by Experts

Given lines are
$L_{1} (x, y) = 2 x + 3 y - 1 = 0$
$L_{2} (x, y) = 5 x - 6 y - 1 = 0$
$L_{3} (x, y) = x + 2 y - 3 = 0$
Draw these lines on coordinate axes.

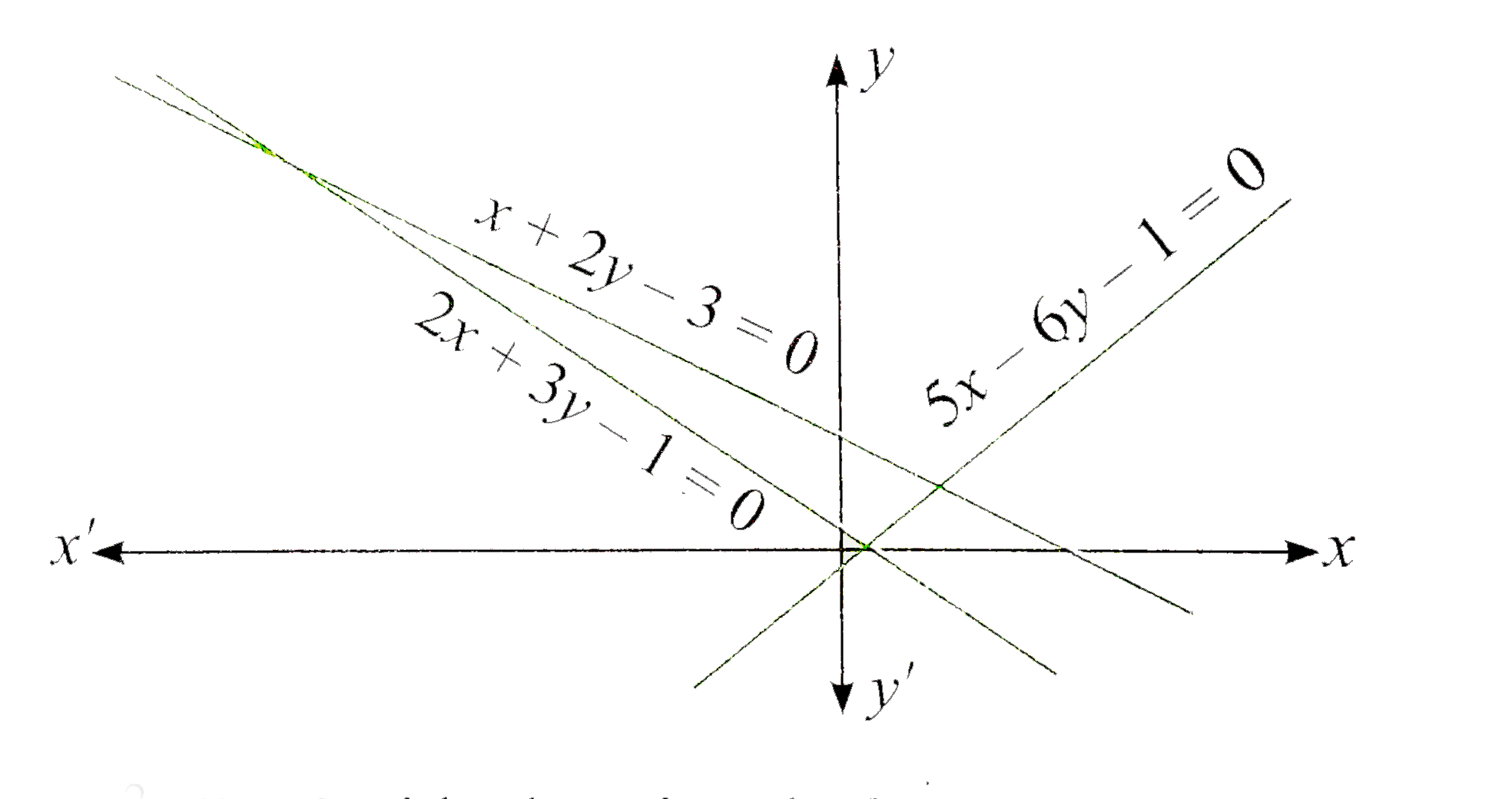
Point $P (α, α^{2})$ lies inside the triangle formed by these lines.
Clearly, from the figure, origin and point P lie on the opposite side w.r.t 2x+3y-1=0.
$L_{1} (0, 0) = - 1 < 0$
So, we must have
$L_{1} (α, α^{2}) = 2 α + 3 α^{2} - 1 > 0$
$\Rightarrow (3 α - 1) (α + 1) > 0$
$\Rightarrow α < - 1 or α > 1 / 3 (1)$
Also, origin and point P lie on the same side w.r.t line
x+2y-3=0.
$L_{3} (0, 0) = - 3 < 0$
So, we must have $L_{3} (α, α^{2}) = α + 2 α^{2} - 3 < 0$
$\Rightarrow (2 α + 3) (α - 1) < 0$
$\Rightarrow - 3 / 2 < α < 1 (2)$
Further origin and point P lie on the same side w.r.t. line
5x-6y-1=0.
$\Rightarrow L_{2} (0, 0) = - 1 < 0$
So, we must have
$L_{2} (α, α^{2}) = 5 α - 6 α^{2} - 1 < 0$
$\Rightarrow 6 α^{2} - 5 α + 1 > 0$
$\Rightarrow (3 α - 1) (2 α - 1) > 0$
$\Rightarrow α < 1 / 3 or α > 1 / 2 (3)$
From (1), (2) and (3), common values of $α$ are (-3/2,-1) $\cup$ (1/2,1).

|

Updated on:21/07/2023

Class 12 MATHS STRAIGHT LINES

Topper's Solved these Questions

Similar Questions

CENGAGE-STRAIGHT LINES-JEE Advanced Previous Year

Home
Ask Doubt
Profile