Determine the integer whose product with −1 is (i) 58 (ii) 0 (iii) -225
To solve the question, we need to determine the integer whose product with −1 gives us the specified values: 58, 0, and -225. Let's break this down step by step.
1. We start with the equation:
\(
-1 \times x = 58
\)
where \( x \) is the integer we are trying to find.
2. To isolate \( x \), we can divide both sides of the equation by −1:
\(
x = \frac{58}{-1}
\)
3. Simplifying the right side gives:
\(
x = -58
\)
Thus, the integer whose product with −1 is 58 is -58.
---
(ii) Determine the integer whose product with −1 is 0:
1. We start with the equation:
\(
-1 \times x = 0
\)
2. To find \( x \), we divide both sides by −1:
\(
x = \frac{0}{-1}
\)
3. Simplifying the right side gives:
\(
x = 0
\)
Thus, the integer whose product with −1 is 0 is 0.
---
(iii) Determine the integer whose product with −1 is -225:
1. We start with the equation:
\(
-1 \times x = -225
\)
2. To isolate \( x \), we divide both sides by −1:
\(
x = \frac{-225}{-1}
\)
3. Simplifying the right side gives:
\(
x = 225
\)
Thus, the integer whose product with −1 is -225 is 225.
---
Final Answers:
- (i) -58
- (ii) 0
- (iii) 225
\(
-1 \times x = 58
\)
where \( x \) is the integer we are trying to find.
\(
x = \frac{58}{-1}
\)
\(
x = -58
\)
\(
-1 \times x = 0
\)
\(
x = \frac{0}{-1}
\)
\(
x = 0
\)
\(
-1 \times x = -225
\)
\(
x = \frac{-225}{-1}
\)
\(
x = 225
\)
- (i) -58
- (ii) 0
- (iii) 225
Topper's Solved these Questions
Similar Questions
Knowledge Check
Calculate the LCM of two positive integers whose product is 108 and HCF is 3
A72B36C18D9
Express each of the following integers as a product of its prime factors: (i) 420 (ii) 468 (iii) 945 (iv) 7325
View SolutionExpress each of the following positive integers as the product of its prime factors. 38255005 (iii) 7429
View SolutionWhat is the slope of the line whose inclination is :
(i)0∘ (ii)60∘ (iii)150∘ ?
View SolutionMark the following integers on a number line: (i) 7 (ii) −4 (iii) 0
View SolutionFind the inclination of the line whose slope is :
(i)0 (ii)14 (iii)3.
View Solution
How would the ratio of products change if.
(i) R=Et
(ii)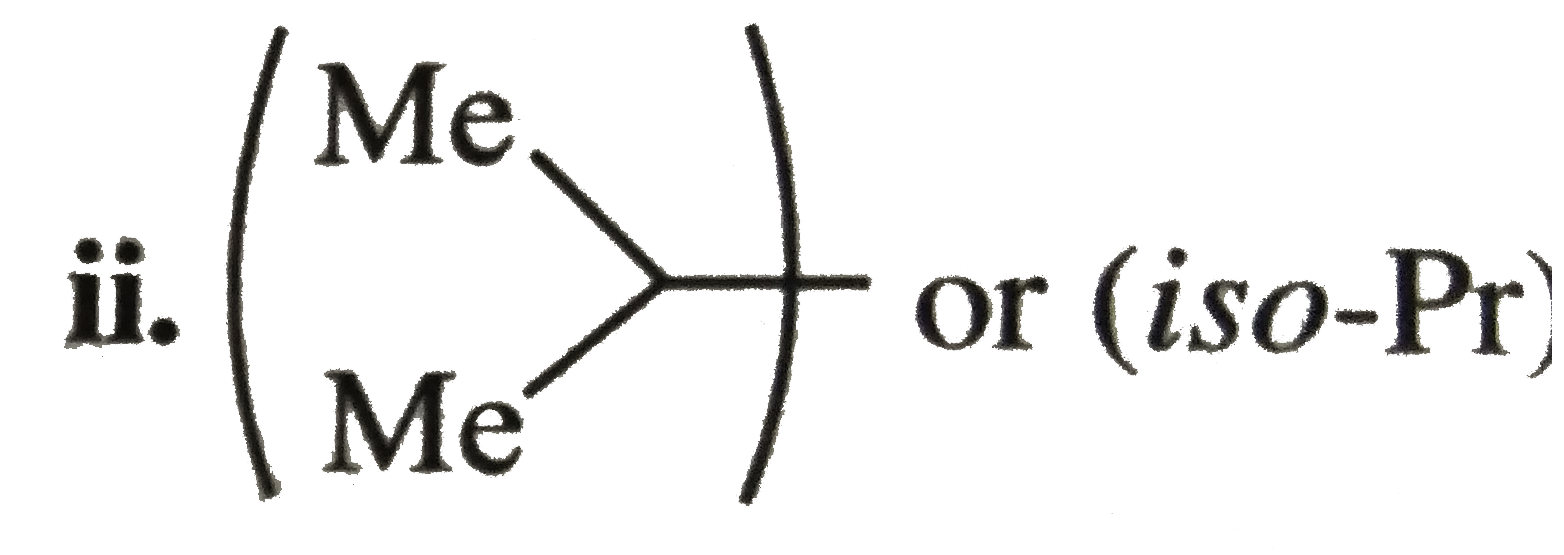
(iii)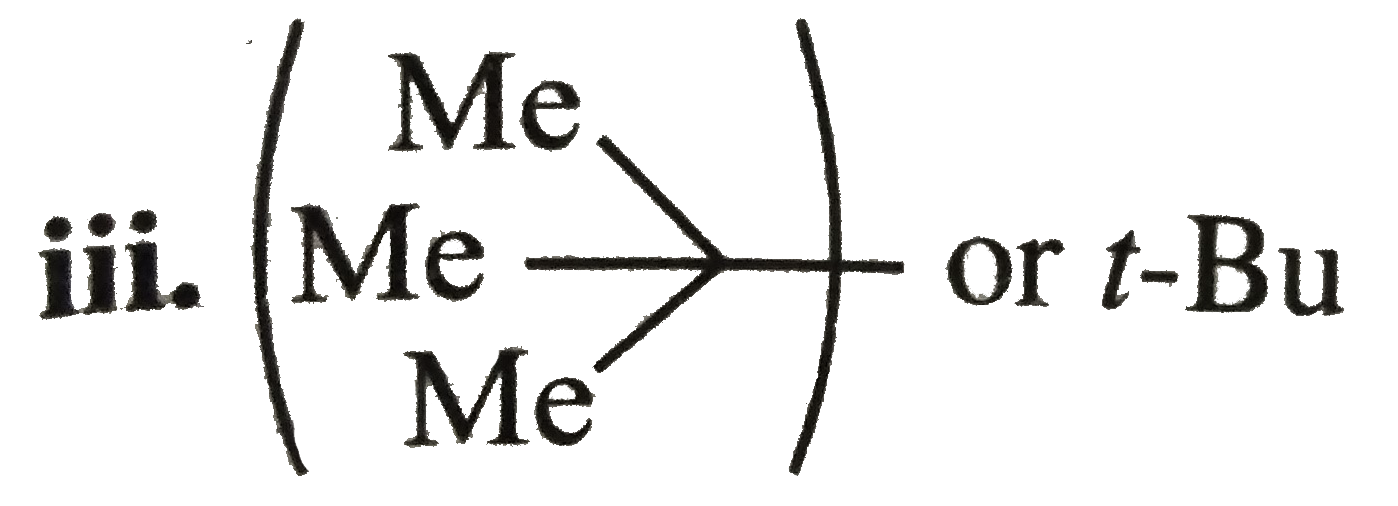 .
.
View SolutionFind the inclination of the lines whose slopes are as follows :
(i)√3 (ii)1 (iii) −1√3
View Solution
