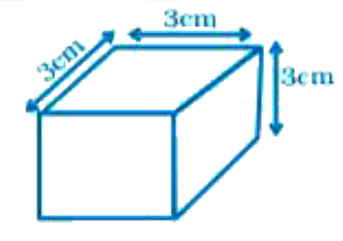
Determine the number of edges, vertices and faces in the fig.
Video Solution
Text Solution
The correct Answer is:The measure of the edges are not needed.
|
Answer
Step by step video & image solution for Determine the number of edges, vertices and faces in the fig. by Maths experts to help you in doubts & scoring excellent marks in Class 7 exams.
Updated on:21/07/2023Topper's Solved these Questions
- PRACTICAL GEOMETRY SYMMETRY AND VISUALISING SOLID SHAPESBOOK - NCERT EXEMPLARCHAPTER - PRACTICAL GEOMETRY SYMMETRY AND VISUALISING SOLID SHAPESEXERCISE - THINK AND DISCUSS
6 Videos
- PRACTICAL GEOMETRY SYMMETRY AND VISUALISING SOLID SHAPESBOOK - NCERT EXEMPLARCHAPTER - PRACTICAL GEOMETRY SYMMETRY AND VISUALISING SOLID SHAPESEXERCISE - EXERCISE
108 Videos
- PERIMETER AND AREABOOK - NCERT EXEMPLARCHAPTER - PERIMETER AND AREAEXERCISE - Think and Discuss
7 Videos
- RATIONAL NUMBERSBOOK - NCERT EXEMPLARCHAPTER - RATIONAL NUMBERSEXERCISE - Application
2 Videos
Similar Questions
Knowledge Check
Faces : The flat surface of any solid is called face.
Edges : Line segments where two faces meet is called an edge.
Vertices : Corners of the solid are its vertices.
Find the number of edges and vertices respectively of octahedron.A12, 6B6, 12C8, 12D12, 8If x, y and z represent the number of faces, number of vertices and number of edges respectively of a polyhedron, then which of the following is true ?
Ay−2=z+xBx−2=z−yCx+2=z−yDz−2=x−yIf a, b and c are respectively the number of faces, edges and vertices of a pentagonal pyramid, then the value of (a+b+c2)2 - 2 is
A−15B2C1.75D−1
Make a conjuecture What do you think is true about the relationship between the number of vertices, edges and faces of a polyhedron ?
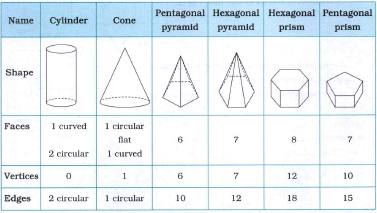
View SolutionComplete the table below by writing the number of faces, edges and vertices each figure has :
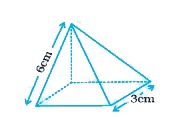
View SolutionWater the number of vertices, edges and faces of a pentagonal pyramid ?
View SolutionWrite the number of vertices, edges and faces of a pentagonal prism ?
View SolutionIdentify the given figure. Also write number of faces, vertices and edges.

View Solution