Determine the number of zeroes of the polynomial x4−1
To determine the number of zeroes of the polynomial x4−1, we can follow these steps:
Step 1: Set the polynomial equal to zero
We start by setting the polynomial equal to zero:
x4−1=0
Step 2: Factor the polynomial
Next, we can factor the polynomial using the difference of squares:
x4−1=(x2−1)(x2+1)
Step 3: Factor further
Now, we can factor x2−1 further since it is also a difference of squares:
x2−1=(x−1)(x+1)
Thus, we can rewrite the polynomial as:
(x−1)(x+1)(x2+1)=0
Step 4: Solve for zeroes
Now we will solve each factor for zero:
1. From x−1=0, we get:
x=1
2. From x+1=0, we get:
x=−1
3. From x2+1=0, we can rearrange to find:
x2=−1
Taking the square root of both sides gives:
x=iandx=−i
Step 5: Count the number of zeroes
Now we can summarize the zeroes we found:
- From x−1=0: x=1
- From x+1=0: x=−1
- From x2+1=0: x=i and x=−i
Thus, the total number of zeroes is:
1,−1,i,−i
This gives us a total of 4 zeroes.
Conclusion
The number of zeroes of the polynomial x4−1 is 4.
---
We start by setting the polynomial equal to zero:
x4−1=0
Next, we can factor the polynomial using the difference of squares:
x4−1=(x2−1)(x2+1)
Now, we can factor x2−1 further since it is also a difference of squares:
x2−1=(x−1)(x+1)
Thus, we can rewrite the polynomial as:
(x−1)(x+1)(x2+1)=0
Now we will solve each factor for zero:
1. From x−1=0, we get:
x=1
2. From x+1=0, we get:
x=−1
3. From x2+1=0, we can rearrange to find:
x2=−1
Taking the square root of both sides gives:
x=iandx=−i
Now we can summarize the zeroes we found:
- From x−1=0: x=1
- From x+1=0: x=−1
- From x2+1=0: x=i and x=−i
1,−1,i,−i
This gives us a total of 4 zeroes.
The number of zeroes of the polynomial x4−1 is 4.
Topper's Solved these Questions
- BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 2 EXERCISE - SECTION - B7videos
SAMPLE PAPER 2
- BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 2 EXERCISE - SECTION - C11videos
SAMPLE PAPER 2
- BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 2 EXERCISE - SECTION - A (Fill in the blanks )5videos
SAMPLE PAPER 2
- BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 13EXERCISE - PART - B (SECTION - V)4videos
SAMPLE PAPER 13
- BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 2019EXERCISE - Section - D12videos
SAMPLE PAPER 2019
Similar Questions
Knowledge Check
- Question 1 - Select One
Numbers of zeroes of the zero polynomial is
A0B1C2DInfinite - Question 2 - Select One
What will be the number of real zeros of the polynomial x2+1 ?
A-1B0C1D2 - Question 3 - Select One
One of the zeroes of the polynomial 2x2+7x−4 is
A2B12C−12D−2
Find zeroes of the polynomial 5x2−4−8x.
View SolutionDetermine the zeroes of the polynomial p(x)=x3−2x2. Also verify the relationship between the zeroes and the coefficient.
View SolutionFind the number of zeroes, for the polynomial p(x) shown in the graph below :
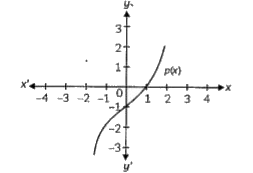 View Solution
View SolutionFind the number of zeroes, for the polynomial p(x) shown in the graph below:
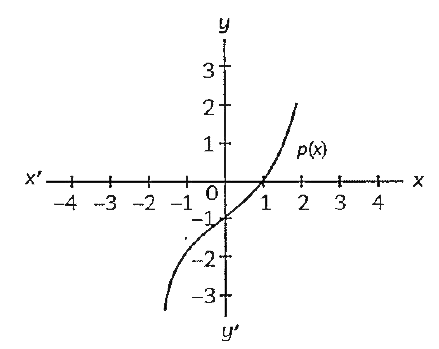 View Solution
View SolutionFind the number of zeroes , for the polynomial p(x) shown in the group below :
 View Solution
View Solution

