Does Euclid’s fifth postulate imply the existence of parallel lines? Explain.
To determine whether Euclid's fifth postulate implies the existence of parallel lines, we can analyze the postulate step by step.
1. Understanding Euclid's Fifth Postulate:
- Euclid's fifth postulate states that if a straight line intersects two other straight lines and the sum of the interior angles on one side is less than two right angles (180 degrees), then the two lines will meet on that side when extended.
2. Analyzing the Conditions:
- If the sum of the interior angles on one side (let's call them angle 1 and angle 2) is less than 180 degrees, the two lines will eventually intersect on that side.
- If the sum of the angles on the other side (angle 3 and angle 4) is greater than 180 degrees, the lines will also intersect on that side.
3. Identifying the Parallel Condition:
- The only scenario where the two lines do not meet is when the sum of the angles on one side (angle 1 + angle 2) is exactly equal to 180 degrees, and the sum of the angles on the other side (angle 3 + angle 4) is also equal to 180 degrees.
- In this case, the two lines do not meet on either side, which means they are parallel.
4. Conclusion:
- Therefore, Euclid's fifth postulate does imply the existence of parallel lines. When the angles are equal to 180 degrees on both sides, it indicates that the lines will never intersect, thus confirming that they are parallel.
- Euclid's fifth postulate states that if a straight line intersects two other straight lines and the sum of the interior angles on one side is less than two right angles (180 degrees), then the two lines will meet on that side when extended.
- If the sum of the interior angles on one side (let's call them angle 1 and angle 2) is less than 180 degrees, the two lines will eventually intersect on that side.
- If the sum of the angles on the other side (angle 3 and angle 4) is greater than 180 degrees, the lines will also intersect on that side.
- The only scenario where the two lines do not meet is when the sum of the angles on one side (angle 1 + angle 2) is exactly equal to 180 degrees, and the sum of the angles on the other side (angle 3 + angle 4) is also equal to 180 degrees.
- In this case, the two lines do not meet on either side, which means they are parallel.
- Therefore, Euclid's fifth postulate does imply the existence of parallel lines. When the angles are equal to 180 degrees on both sides, it indicates that the lines will never intersect, thus confirming that they are parallel.
Topper's Solved these Questions
- INTRODUCTION TO EUCLIDS GEOMETRYBOOK - NCERT ENGLISHCHAPTER - INTRODUCTION TO EUCLIDS GEOMETRYEXERCISE - Exercise 5.1
7 Videos
- INTRODUCTION TO EUCLIDS GEOMETRYBOOK - NCERT ENGLISHCHAPTER - INTRODUCTION TO EUCLIDS GEOMETRYEXERCISE - Exercise 5.1
7 Videos
- HERONS FORMULABOOK - NCERT ENGLISHCHAPTER - HERONS FORMULAEXERCISE - Solved Examples
6 Videos
- LINEAR EQUATIONS IN TWO VARIABLESBOOK - NCERT ENGLISHCHAPTER - LINEAR EQUATIONS IN TWO VARIABLESEXERCISE - Exercise 4.1
2 Videos
Similar Questions
How would you rewrite Euclid’s fifth postulate so that it would be easier to understand?
View SolutionAttempt to prove Euclid 's fifth postulate using the other postulates and axioms led to the discovery of several other geometries.
View Solution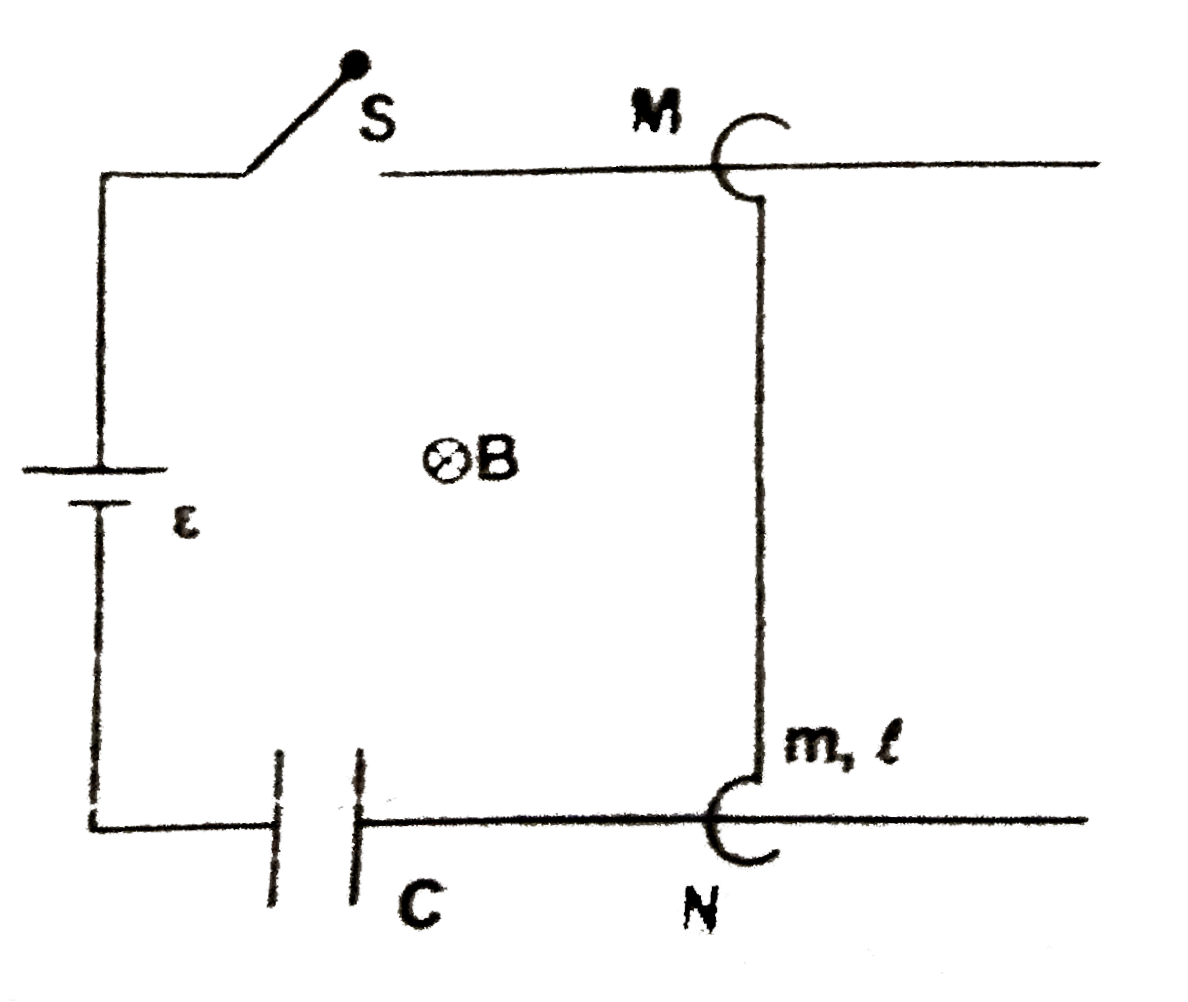
A conducting rod MN of mass m and length 'l' is placed on parallel smooth conducting rails connected to an uncharged capacitor of capacitance C and a battery of emf ε as shown. A uniform magnetic field B is existing perpendicular to the plane of the rails. The steady state velocity acquired by the conducting rod MN after closing switch S is (neglect the resistance of the parallel rails and the conducting rod)
View SolutionHow does industrial melanism support Darwin’s theory of N atural Selection? Explain.
View SolutionStatement-1 : The Bohr model of the hydrogen atom does not explain the fine structure of spectral lines.
and
Statement-2 : The Bohr model does not take into account the spin of the electron
View SolutionFig. shows some of the electric field lines due to three point charges arranged along the vertical axis. All three charges have the same magnitude.
(a) What are the signs of each of the three charges? Explain your reasoning.
(b) At what points(s) is the magnitude of the electric field the smallest? Explain your reasoning. Explain how the fields produced by each individual point charge combine to give a small net field at this point or points.
(c ) Two point charges q and -q are placed at a distance d apart. What are the points at which the resultant electric field is parallel to the line joining the two charge?
 .
.
View SolutionDefine the law of multiple proportions, Explain it with examples. How does this law point to the existence of atoms?
View SolutionConsider two ‘postulates’ given below:(i) Given any two distinct points A and B, there exists a third point C which is in between A and B.(ii) There exist at least three points that are not on the same line. Do these postulates contain any undefined terms? Are these postulates consistent? Do they follow from Euclid’s postulates? Explain.
View SolutionState and explain the main postulates of valence bond theory. How does this theory explain the shapes of the following molecules?
HF,N2,H2SandPH3
View SolutionWhy does a light ray incident on a rectangular glass slab immersed in any medium emerges parallel to itself ? Explain using a diagram.
View Solution
