Does there exist a GP containing 27,8 and 12 as threee of its terms ? If it exist, how many such progressions are possible ?
To determine if there exists a geometric progression (GP) containing the terms 27, 8, and 12, we can follow these steps:
Step 1: Define the Terms in the GP
Assume that the terms 27, 8, and 12 correspond to the Pth, Qth, and Rth terms of the GP, respectively. Let:
- TP=27
- TQ=8
- TR=12
Let A be the first term and r be the common ratio of the GP. Then we can express the terms as:
- TP=ArP−1
- TQ=ArQ−1
- TR=ArR−1
Step 2: Set Up the Ratios
From the expressions above, we can set up the following ratios:
1. TPTQ=278=ArP−1ArQ−1
- This simplifies to:
rP−Q=278
2. TQTR=812=ArQ−1ArR−1
- This simplifies to:
rQ−R=23
Step 3: Express the Ratios in Terms of r
From the first ratio, we can express rP−Q:
rP−Q=(32)3
From the second ratio, we can express rQ−R:
rQ−R=23
Step 4: Relate the Exponents
Now we can relate the exponents:
1. From rP−Q=(32)3, we have:
P−Q=3logr(32)
2. From rQ−R=23, we have:
Q−R=logr(23)
Step 5: Solve for the Relationships
We can express R in terms of Q:
R=Q−logr(23)
Substituting this back into the first equation, we can find relationships between P, Q, and R.
Step 6: Conclusion
Since we have a single equation with three variables, we can assign various values to P, Q, and R while maintaining the relationships derived above. This indicates that there are infinitely many GPs that can include the terms 27, 8, and 12.
Final Answer
Yes, there exists a GP containing the terms 27, 8, and 12, and there are infinitely many such progressions possible.
---
Assume that the terms 27, 8, and 12 correspond to the Pth, Qth, and Rth terms of the GP, respectively. Let:
- TP=27
- TQ=8
- TR=12
- TP=ArP−1
- TQ=ArQ−1
- TR=ArR−1
From the expressions above, we can set up the following ratios:
1. TPTQ=278=ArP−1ArQ−1
- This simplifies to:
rP−Q=278
- This simplifies to:
rQ−R=23
From the first ratio, we can express rP−Q:
rP−Q=(32)3
From the second ratio, we can express rQ−R:
rQ−R=23
Now we can relate the exponents:
1. From rP−Q=(32)3, we have:
P−Q=3logr(32)
Q−R=logr(23)
We can express R in terms of Q:
R=Q−logr(23)
Substituting this back into the first equation, we can find relationships between P, Q, and R.
Since we have a single equation with three variables, we can assign various values to P, Q, and R while maintaining the relationships derived above. This indicates that there are infinitely many GPs that can include the terms 27, 8, and 12.
Yes, there exists a GP containing the terms 27, 8, and 12, and there are infinitely many such progressions possible.
Topper's Solved these Questions
Similar Questions
Knowledge Check
How many geometric progressios is/are possible containing 27.8 and 12 as three of its/their terms ?
AOneBTwoCFourDInfinitely manyCompound X can exist in how many orientations ?
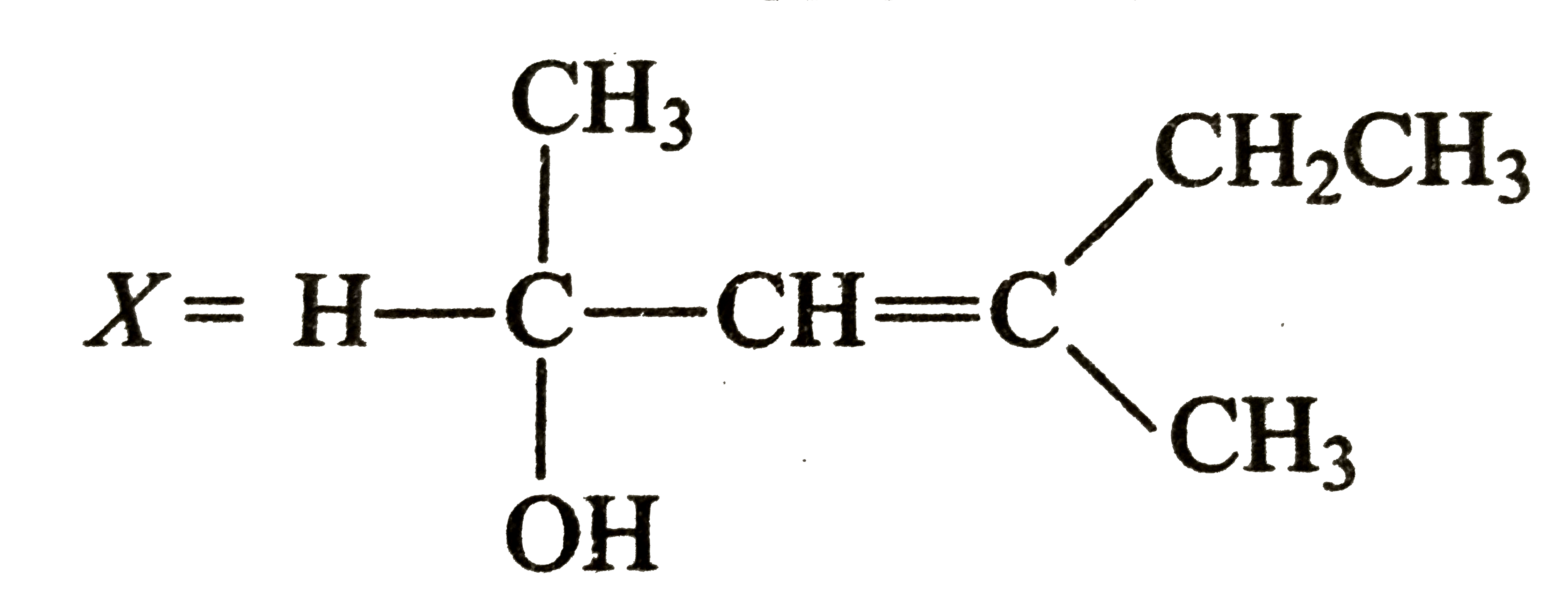 A1B2C3D4
A1B2C3D4If the second term of GP is 2 and the sum of its infinite terms is 8, then the GP is:
AA)8,2,12,18 . . .BB)10,2,25,225CC)4,2,1,12,122 . . .DD)6,3,32,34
In an increasing G.P. , the sum of the first and the last term is 66, the product of the second and the last but one is 128 and the sum of the terms is 126. How many terms are there in the progression?
View SolutionThere are infinite geometric progressions of for which 27,8 and 12 are three of its terms (not necessarily consecutive). Statement 2: Given terms are integers.
View SolutionGlucose exists in how many forms in equilibrium?
View SolutionThe first term of a GP is 27 and its 8th terms is 181. Find the sum of its first 10 terms.
View SolutionThe sum of an infinity decreasing G.P is equal to 4 and the sum of the cubes of its terms is equal to 64/. Then 5th term of the progression is :
View Solution
