Draw a line l. Construct a line m parallel to line l at a distance of 4 cm.
Step-by-Step Solution:
1. Draw Line L:
- Use a ruler to draw a horizontal line. Label it as line L.
2. Select Points on Line L:
- Choose a point A on line L.
- Choose another point B on line L, ensuring that points A and B are not too close to each other.
3. Construct Arcs from Point A:
- Place the compass pointer at point A and draw an arc above and below line L. This will create two intersection points with the vertical lines.
4. Extend the Compass:
- Without changing the compass width, place the compass pointer at the points where the arcs intersect the vertical lines, and draw arcs on both sides.
5. Label Intersection Point:
- Let the intersection of these arcs be point T'.
6. Draw Line from T' to A:
- Use a ruler to draw a line connecting point T' to point A.
7. Construct Arcs from Point B:
- Repeat the same process for point B. Place the compass pointer at point B and draw arcs above and below line L.
8. Extend the Compass Again:
- Without changing the compass width, place the compass pointer at the intersection points of the arcs and draw arcs on both sides.
9. Label Intersection Point:
- Let the intersection of these arcs be point T.
10. Draw Line from T to B:
- Use a ruler to draw a line connecting point T to point B.
11. Set Compass to 4 cm:
- Adjust the compass to a width of 4 cm.
12. Draw Arc from Point B:
- Place the compass pointer at point B and draw an arc on line BT, marking the intersection point as B'.
13. Draw Arc from Point A:
- Now, place the compass pointer at point A and draw an arc on line AT', marking the intersection point as A'.
14. Join Points A' and B':
- Use a ruler to draw a line connecting points A' and B'. This line is parallel to line L and is at a distance of 4 cm from it.
Final Result:
- The line M (A'B') is now constructed parallel to line L (AB) at a distance of 4 cm.
- Use a ruler to draw a horizontal line. Label it as line L.
- Choose a point A on line L.
- Choose another point B on line L, ensuring that points A and B are not too close to each other.
- Place the compass pointer at point A and draw an arc above and below line L. This will create two intersection points with the vertical lines.
- Without changing the compass width, place the compass pointer at the points where the arcs intersect the vertical lines, and draw arcs on both sides.
- Let the intersection of these arcs be point T'.
- Use a ruler to draw a line connecting point T' to point A.
- Repeat the same process for point B. Place the compass pointer at point B and draw arcs above and below line L.
- Without changing the compass width, place the compass pointer at the intersection points of the arcs and draw arcs on both sides.
- Let the intersection of these arcs be point T.
- Use a ruler to draw a line connecting point T to point B.
- Adjust the compass to a width of 4 cm.
- Place the compass pointer at point B and draw an arc on line BT, marking the intersection point as B'.
- Now, place the compass pointer at point A and draw an arc on line AT', marking the intersection point as A'.
- Use a ruler to draw a line connecting points A' and B'. This line is parallel to line L and is at a distance of 4 cm from it.
- The line M (A'B') is now constructed parallel to line L (AB) at a distance of 4 cm.
Topper's Solved these Questions
- BOOK - ICSECHAPTER - CONSTRUCTIONS EXERCISE - TRY THIS12videos
CONSTRUCTIONS
- BOOK - ICSECHAPTER - CONSTRUCTIONS EXERCISE - EXERCISE 14.118videos
CONSTRUCTIONS
- BOOK - ICSECHAPTER - CONSTRUCTION EXERCISE - EXERCISE18videos
CONSTRUCTION
- BOOK - ICSECHAPTER - DATA HANDLING AND MEASURES OF CENTRAL TENDENCYEXERCISE - TRY THIS19videos
DATA HANDLING AND MEASURES OF CENTRAL TENDENCY
Similar Questions
Knowledge Check
- Question 1 - Select One
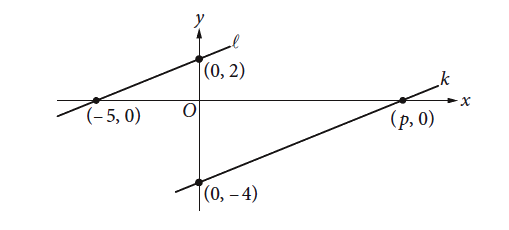
In the xy-plane above, line l is parallel to line k. What is the value of p ?A4B5C8D10 - Question 2 - Select One

In the figure above, lines l and m are parallel and lines s and t are parallel. If the measure of ∠1 is 35∘, what is the measure of ∠2 ?A35∘B55∘C70∘D145∘
Draw two parallel lines at a distance 5 cm apart.
View SolutionDraw a straight line AB=6.5 cm. draw another line which is parallel to AB at a distance of 2.8 cm from it.
View SolutionConstruct an angle PQR=80∘. Draw a line parallel to PQ at a distance of 3 cm from it and another line parallel to QR at a distance of 3.5 cm from it. Mark the point of intersection of these parallel lines as A.
View SolutionDraw a line segment PQ. Take a point S outside this line, and draw a line parallel to PQ, through S. Join S with P. Construct a line parallel to SP, through Q. Mark the point at which it meets the parallel line through S at R. What is the shape of PQRS ?
View SolutionLet R be a relation on the set of all lines in a plane defined by (l1, l2)∈R <=> line l1 is parallel to line l2 . Show that R is an equivalence relation.
View SolutionDraw a line l. Take any point A outside the line. Draw a line through A, parallel to line l.
View Solution

