Draw an angle bisector of 75°.
To construct the angle bisector of a 75° angle, follow these step-by-step instructions:
Step 1: Draw a Line Segment
- Draw a line segment AB of any convenient length. Label the endpoints as A and B.
Step 2: Construct a 75° Angle
- Using a protractor, place the center point of the protractor at point A.
- Locate the 75° mark on the protractor and make a small mark on the paper.
- Label this point as C.
- Draw a ray AC that extends through point C, forming a 75° angle with line segment AB.
Step 3: Draw Arcs from Points on the Angle
- Place the compass point on point A and draw an arc that intersects ray AC. Let this intersection point be labeled as P.
- Without changing the compass width, place the compass point on point C and draw another arc that intersects ray AC. Let this intersection point be labeled as Q.
Step 4: Mark the Intersection Point
- The two arcs you drew from points P and Q will intersect at a point. Label this intersection point as Z.
Step 5: Draw the Angle Bisector
- Finally, draw a straight line from point A to point Z. This line AZ is the angle bisector of the 75° angle.
Summary
You have successfully constructed the angle bisector of a 75° angle by following these steps.
---
- Draw a line segment AB of any convenient length. Label the endpoints as A and B.
- Using a protractor, place the center point of the protractor at point A.
- Locate the 75° mark on the protractor and make a small mark on the paper.
- Label this point as C.
- Draw a ray AC that extends through point C, forming a 75° angle with line segment AB.
- Place the compass point on point A and draw an arc that intersects ray AC. Let this intersection point be labeled as P.
- Without changing the compass width, place the compass point on point C and draw another arc that intersects ray AC. Let this intersection point be labeled as Q.
- The two arcs you drew from points P and Q will intersect at a point. Label this intersection point as Z.
- Finally, draw a straight line from point A to point Z. This line AZ is the angle bisector of the 75° angle.
You have successfully constructed the angle bisector of a 75° angle by following these steps.
Topper's Solved these Questions
- CONSTRUCTIONSBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - CONSTRUCTIONSEXERCISE - (PRACTICE-TEST) SECTION-C
1 Videos
- CONSTRUCTIONSBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - CONSTRUCTIONSEXERCISE - (PRACTICE-TEST) SECTION-A
4 Videos
- Co-ordinate GeometryBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - Co-ordinate GeometryEXERCISE - PRACTICE-TEST (Coordinate Geometry) SECTION-D
1 Videos
- INTRODUCTION TO TRIGONOMETRYBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - INTRODUCTION TO TRIGONOMETRYEXERCISE - PRACTICS-TEST (SECTION-D)
1 Videos
Similar Questions
Knowledge Check
ABCDE is a regular pentagon. Angle bisector of ∠BAE meets CD at m. angle bisector of ∠BCD meets AM at P. Find the ∠CPM= ?
A30B35C36D60Find the value of ∠A. If BD is an interior angle bisector of ∠B and DC is an exterior angle bisector of ∠C.
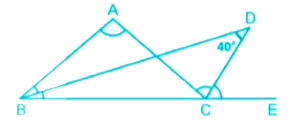 A70∘B60∘C80∘D110∘
A70∘B60∘C80∘D110∘The point of intersection of the angle bisectors of a triangle is :
AorthocentreBcentroidCincentreDcircumcentre
Family of lines continued and angle bisector
View Solution3. Draw an obtuse-angled triangle and a right-angled triangle. Find the points of the concurrence of the angle bisectors of each angle
View SolutionIn parallelogram ABCD, the angle bisector of ∠A bisects BC. Will angle bisector of B also bisect AD? Give reason.
View SolutionAngle bisectors| problems
View SolutionThe point of intersection of the angle bisectors of a triangle is :
View Solution
