Draw nets for each of the following polyhedrons: (Figure) A cube (ii) A triangular prism A hexagonal prism (iv) A pentagonal pyramid
To draw the nets for the given polyhedrons, we will follow these steps for each shape:
1. Net of a Cube:
- A cube consists of 6 square faces.
- To create the net, draw one square in the center.
- Attach one square to each of the four sides of the central square.
- Finally, add one square on top or below the central square.
- This arrangement will show all 6 squares connected, forming the net of a cube.
2. Net of a Triangular Prism:
- A triangular prism has 2 triangular faces and 3 rectangular faces.
- Start by drawing one triangle at the top.
- Draw another triangle directly below it, aligned with the first triangle.
- Now, connect the sides of the triangles with three rectangles.
- Each rectangle will connect one side of the top triangle to the corresponding side of the bottom triangle.
- This will give you the net of a triangular prism.
3. Net of a Hexagonal Prism:
- A hexagonal prism has 2 hexagonal faces and 6 rectangular faces.
- Begin by drawing one hexagon at the top.
- Draw another hexagon directly below it.
- Connect the sides of the hexagons with six rectangles.
- Each rectangle will connect one side of the top hexagon to the corresponding side of the bottom hexagon.
- This will form the net of a hexagonal prism.
4. Net of a Pentagonal Pyramid:
- A pentagonal pyramid has 1 pentagonal base and 5 triangular faces.
- Start by drawing a pentagon for the base.
- From each vertex of the pentagon, draw a triangle that meets at a single point above the center of the pentagon.
- This will show all triangular faces connected to the pentagonal base, forming the net of a pentagonal pyramid.
- A cube consists of 6 square faces.
- To create the net, draw one square in the center.
- Attach one square to each of the four sides of the central square.
- Finally, add one square on top or below the central square.
- This arrangement will show all 6 squares connected, forming the net of a cube.
- A triangular prism has 2 triangular faces and 3 rectangular faces.
- Start by drawing one triangle at the top.
- Draw another triangle directly below it, aligned with the first triangle.
- Now, connect the sides of the triangles with three rectangles.
- Each rectangle will connect one side of the top triangle to the corresponding side of the bottom triangle.
- This will give you the net of a triangular prism.
- A hexagonal prism has 2 hexagonal faces and 6 rectangular faces.
- Begin by drawing one hexagon at the top.
- Draw another hexagon directly below it.
- Connect the sides of the hexagons with six rectangles.
- Each rectangle will connect one side of the top hexagon to the corresponding side of the bottom hexagon.
- This will form the net of a hexagonal prism.
- A pentagonal pyramid has 1 pentagonal base and 5 triangular faces.
- Start by drawing a pentagon for the base.
- From each vertex of the pentagon, draw a triangle that meets at a single point above the center of the pentagon.
- This will show all triangular faces connected to the pentagonal base, forming the net of a pentagonal pyramid.
Topper's Solved these Questions
Similar Questions
Draw all lines of symmetry for each of the following figures :
View SolutionDraw the lines of symmetry in each of the following figures.

View SolutionDraw the line (or lines) of symmetry of each of the following figures.
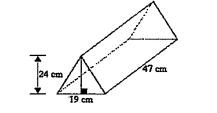
View SolutionFind the volume of the following triangular prism
View SolutionCompute the value of x in each of the following figures: (ii) (iv)
View SolutionDraw the nets of the following
(i) Triangular prism
(ii) Tetrahedron
(iii) Cuboid
View SolutionWrite down the number of faces of each of the following figures:
(i) Cuboid, (ii) Cube, (iii) Triangular prism, (iv) Square pyramid, (v) Tetrahedron
View SolutionWhich of the following is the net for a hexagonal prism?
View SolutionWrite down the number of edges of each of the following figures.
(i) Tetrahedron , (ii) Rectangular pyramid, (iii) Cube, (iv) Triangular prism,
View SolutionWrite down the number of vertices of each of the following figures.
(i) Cuboid, (ii) Square pyramid, (iii) Tetrahedron, (iv) Triangular prism,
View Solution
