Draw the graph of f(x)=secx+cosec x,x∈(0,2π)−{π/2,π,3π/2}
Also find the values of 'a' for which the equation secx+cosec x=a has two distinct root and four distinct roots.
Text Solution
We have f(x)=secx+cosec x,x∈(0,2π)−{π/2,π,3π/2}
Consider each of the intervals (0,π/2),(π/2,π),(π,3π/2),(3π/2,2π)
For x∈(0,π/2)
When x→0+orx→π/2−,secx+cosec x→∞
Also in the 1st quadrant, sec x + cosec x gt 0
f'(x)=secxtanx−cosec xcotx
f'(π/4)=0, so x=π/4 is clearly a point of minima.
f(π/4)=2√2
For x∈(π/2,π)
When x→π/2+,secx+cosec x→−∞
When x→π−,secx+cosec x→∞
Also f'(x)+secxtanx−cosec xcotx>0
Hence f(x) is an increasing function.
f(3π/4)=0
For x∈(π,3π/2)
When x→π+,secx+cosec x→−∞
When x→3π/2−,secx+cosec x→−∞
f'(5π/4)=0, so x=5π/4 is clearly a point of maxima.
f(5π/4)=−2√2
For x∈(3π/2,2π)
When, x→3π/2+,secx+cosec x→∞
When x→2π−,secx+cosec x→−∞
Also f'(x)+secxtanx−cosec xcotx<0
Hence f(x) is a decreasing function.
f(7π/4)=0
From the above discussion, the graph of the function is as shown in the following figure. 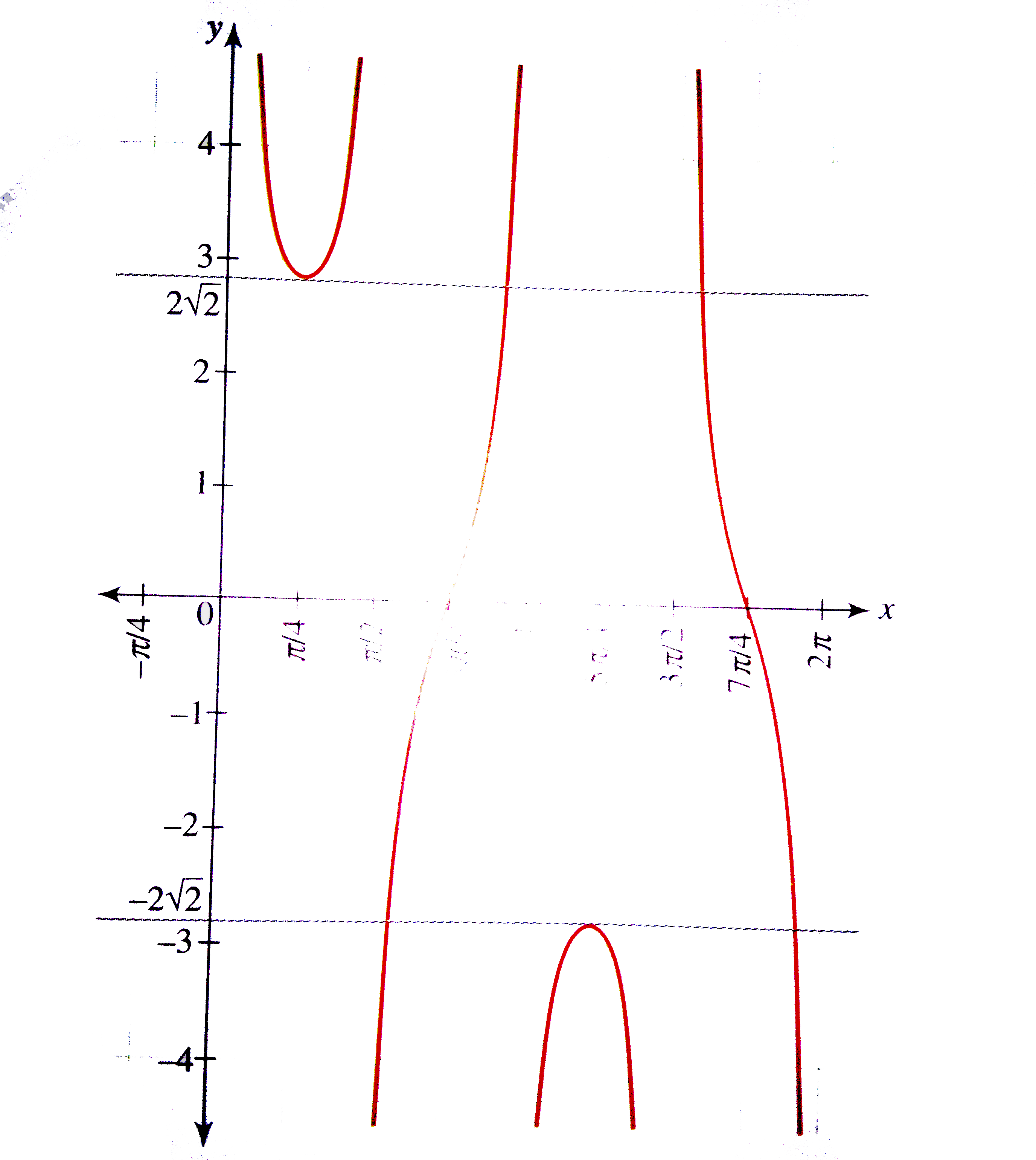
|
Topper's Solved these Questions
- GRAPHS OF TRIGONOMETRIC FUNCTIONSBOOK - CENGAGE PUBLICATIONCHAPTER - GRAPHS OF TRIGONOMETRIC FUNCTIONSEXERCISE - Exercises
22 Videos
- GRAPHS OF ELEMENTARY FUNCTIONS BOOK - CENGAGE PUBLICATIONCHAPTER - GRAPHS OF ELEMENTARY FUNCTIONS EXERCISE - EXERCISES
34 Videos
- HIGHT AND DISTANCE BOOK - CENGAGE PUBLICATIONCHAPTER - HIGHT AND DISTANCE EXERCISE - Archives
3 Videos
Similar Questions
Knowledge Check
Consider the equation
secθ+cosecθ=a,θ∈(0,2π)−{π/2,π,3π/2}
If the equation has no real roots, thenA|a|≥2√2Ba<2√2C|a|<2√2Dnone of theseConsider the equation
secθ+cosecθ=a,θ∈(0,2π)−{π/2,π,3π/2}
If the equation has four distinct real roots, thenA|a|>2√2B|a|<2√2Ca≥−2√2Dnone of theseConsider the equation
secθ+cosecθ=a,θ∈(0,2π)−{π/2,π,3π/2}
If the equation has two distinct real roots, thenA|a|≥2√2Ba<2√2C|a|<2√2Dnone of these
Find the no. of roots of the equation tanx+secx=2cosx in the interval [0,2π]-
View SolutionIf |cotx+cosecx|=|cotx|+|cosecx|,x∈[0,2π], then complete set of values of x is :
View SolutionThe number of values of x∈[−2π,2π] which satisfy the equation cosec x=1+cotx is equal to
View SolutionIf |cotx+cosecx|=|cotx|+cosecx∣,x∈∣[0,2π], then complete set of values of x is :
View SolutionThe value of ∫π/20cosec(x−π3)cosec(x−π6)dx is
View Solution
