Draw the graph of $y = \frac{x - 1}{x - 2}$ . Solution in Tamil

Video Solution

Text Solution

Verified by Experts

We have $y = f (x) = \frac{(x - 1) (6 x - 1)}{2 x - 1}$ .
The domain of the function is $R - {1 / 2}$ .
1. y-intercept $f (0) = 1$ So the graph cuts the y-axis at (0,-1).
2. x-intercept (zeros)
Put $y = 0$ or $(x - 1) (6 x - 1) = 0$
So the graph meets the x-axis at (1/6,0) and (1,0).
3. Asymptotes
Vertical asymptotes
Clearly, the graph has vertical asymptote x = 1/2, where the denominator becomes zero.
Horizontal asymptotes Clearly, the graph has no horizontal asymptote.
Oblique asymptotes
$y = \frac{6 x^{2} - 7 x + 1}{2 x - 1}$
$= 3 x - 2 - \frac{1}{2 x - 1}$
Thus, important points and lines are as follows.

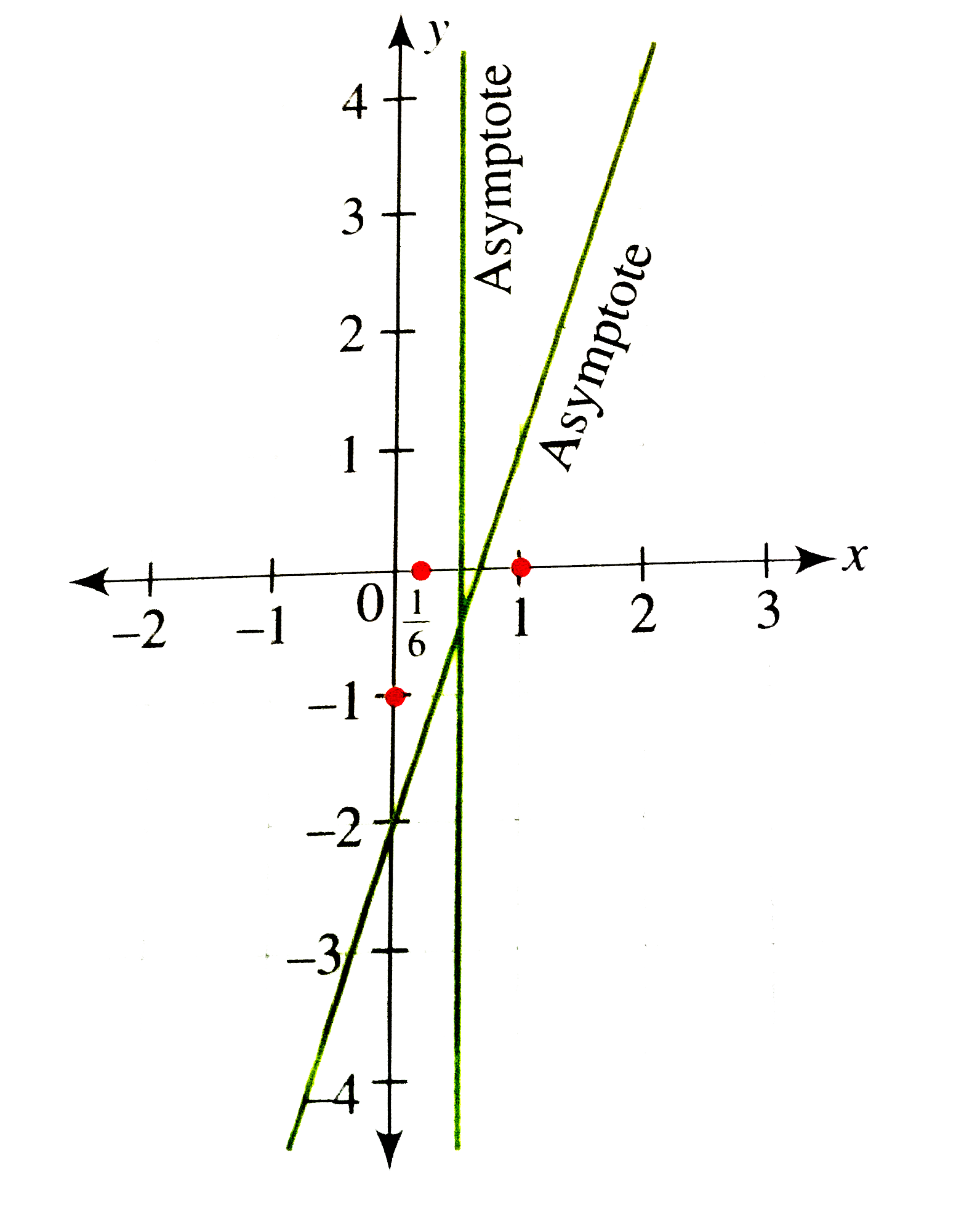
4. Momotonicity/Extremum
$f' (x) = \frac{(12 x - 7) (2 x - 1) - 2 (6 x^{2} - 7 x + 1)}{{(2 x - 1)}^{2}}$
$= \frac{(12 x^{2} - 12 x + 5)}{{(2 x - 1)}^{2}} > 0, \forall x \in R - {1 / 2}$
Hence the function is increasing throughout.
$lim x \to - \infty \frac{(x - 1) (6 x - 1)}{2 x - 1} = - \infty$ and $lim x \to \frac{1^{-}}{2} \frac{(x - 1) (6 x - 1)}{2 x - 1} = \infty$
Thus, f(x) increases from $- \infty$ to $\infty$ when x increases from $- \infty$ to 1/2 crossing the x-axis at (1/6,0) and approaching asymptote $y = 3 x - 2$ to the left of it.
$lim x \to \frac{1^{+}}{2} \frac{(x - 1) (6 x - 1)}{2 x - 1} = - \infty$ and $lim x \to \infty \frac{(x - 1) (6 x - 1)}{2 x - 1} = \infty$
Thus, f(x) increases from $- \infty$ to $\infty$ when x increases from 1/2 to $\infty$ crossing the x-axis at (1,0) . f(x) approaches asymptote $y = 3 x - 2$ to the right of the asymptote.
Hence the graph of $y = f (x)$ can be drawn as shown in the following figure.

|

Updated on:21/07/2023

Class 12 MATHS QUADRATIC EQUATIONS

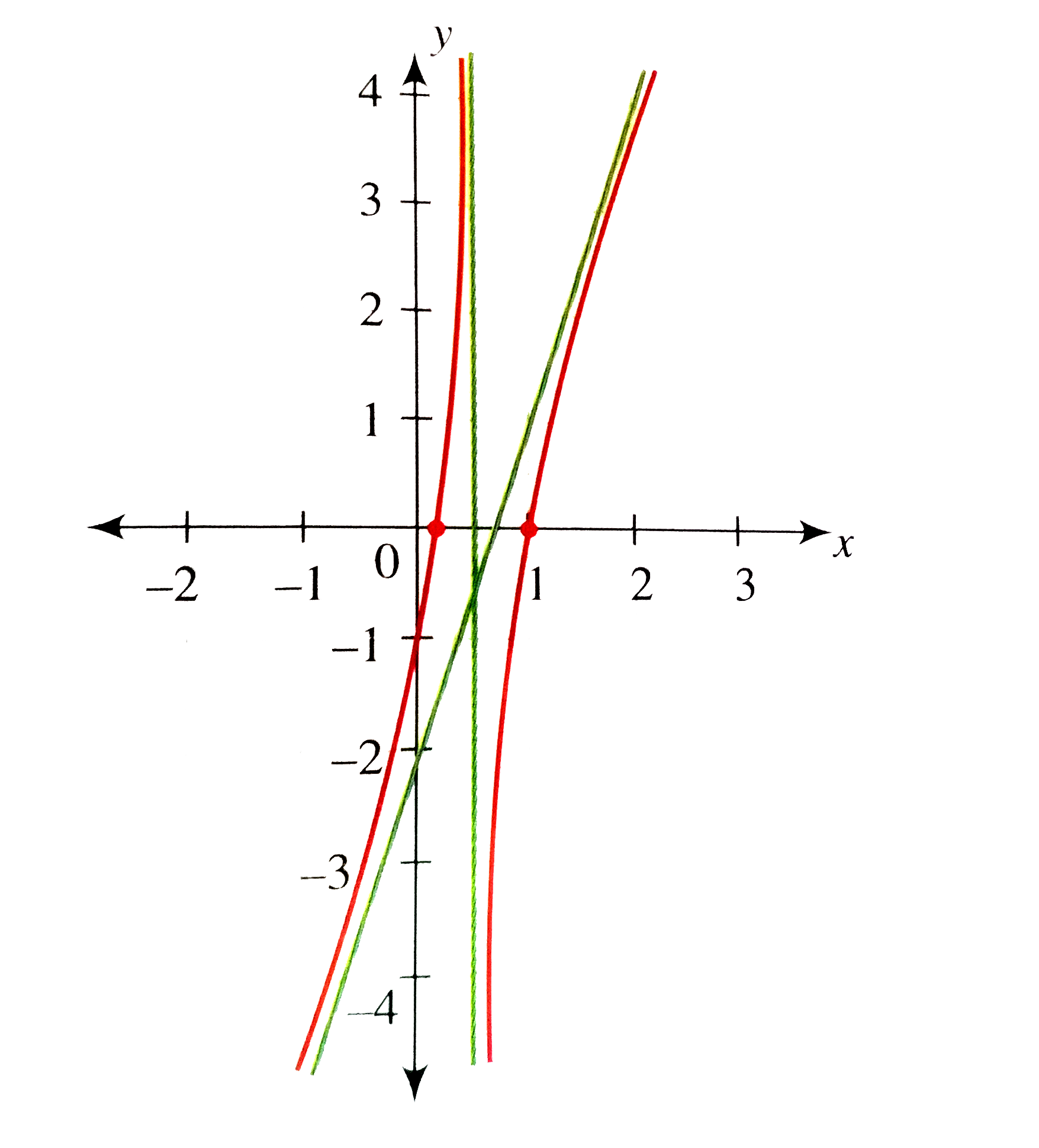
Topper's Solved these Questions

Similar Questions

CENGAGE-GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONS-Exercises

Home
Ask Doubt
Profile