Draw the graph of y=1−x21+x2 and hence draw the graph of y=cos−1.1−x21+x2.
Text Solution
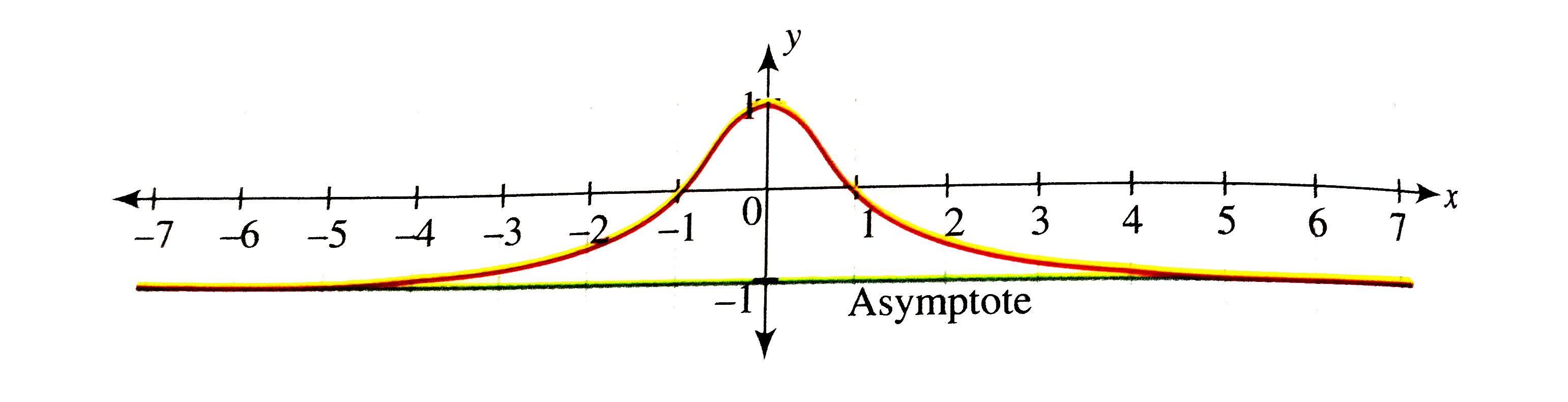
We have y=f(x)=1−x21+x2=21+x2−1
Clearly, the domain is R.
y=f(x) is an even funtion, so the graph is symmetrical about the y-axis.
Let us first draw the graph of rx∈[0,∞).
f(0)=1
f(x)=0∴x=1
limx→∞(21+x2−1)=−1
Thus, from f(0)=1,(21+x2−1) decreases intersecting the x-axis at (1,0) and approaches '-1' as x approaches '∞'.
Also f'(x)=−4x(1+x2)2, so f(x) is differentiable at x = 0.
Hence the graph of y=f(x) is as shown in the following figure.
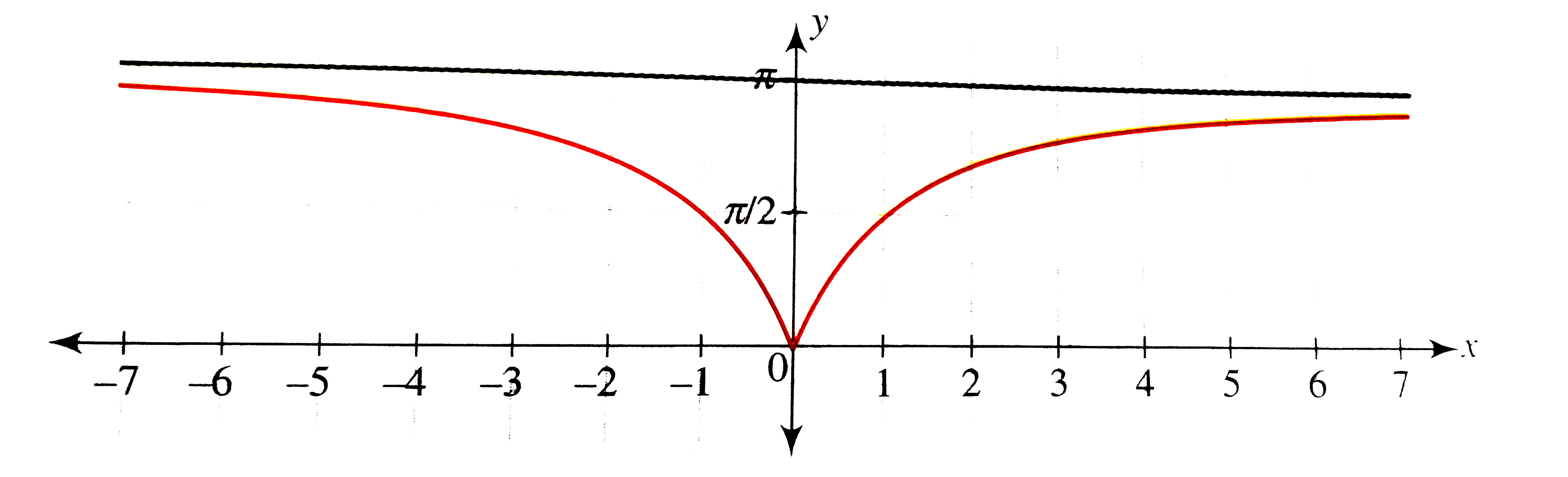
Since the range of 1−x21+x2 is (-1,1), the domain of g(x)=cos−1f(x)=cos−1.1−x21+x2 is also R
g(0)=cos−1(1)=0
and limx→∞cos−1(1−x21+x2)=limx→∞cos−1(21+x2−1)=π
Thus, the value of g(x) increases from '0' and approaches 'π' as x approaches '∞'.
Also g(x) is an enven function, so the graph is symmetrical about the y-axis.
Also g'(x)=f'(x)√1−(f(x))2
g'(0) does not exist as f(0)=1, so g(x) is non-differentiable at x=0.
Hence the graph of y=g(x) can be drawn as shown in the following figure.
|
Updated on:21/07/2023
Related Playlists
- BOOK - CENGAGECHAPTER - GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSEXERCISE - Exercise13videos
GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONS
- BOOK - CENGAGECHAPTER - GRAPHICAL TRANSFORMATIONSEXERCISE - Exercise22videos
GRAPHICAL TRANSFORMATIONS
- BOOK - CENGAGECHAPTER - GRAPHS OF ELEMENTARY FUNCTIONS EXERCISE - Exercise34videos
GRAPHS OF ELEMENTARY FUNCTIONS
Similar Questions
Draw the graph of y=cos−1(x2).
View SolutionDraw the graph of y=x2+1
View SolutionDraw the graph of y=cos−1(2x).
View SolutionDraw the graph of y=cos−1(2x).
View SolutionDraw the graph of y=3x−x31−3x2 and hence the graph of y=tan−1.3x−x31−3x2.
View SolutionDraw the graph of y=sin−1(x2)
View SolutionDraw the graph of y=sin−1(x2)
View SolutionDraw the graph of y=f(x)=x2x2+1.
View SolutionDraw the graph of y=f(x)=x2x2+1.
View SolutionDraw the graph of y=f(x)=x+1x2+1
View Solution

