Draw the graph of y=cot−1x+sec−1x+cosec−1x.
Video Solution
Text Solution
We have y=f(x)=cot−1x+sec−1+x+cosec−1
=cot−1x+π2
Clearly, the domain of the function is (−∞,01)]∪[1,∞)
Therefore, to draw the graph of the function, we shift the graph of y=cot−1x,'π'2 units upward for x∈(−∞,−1]∪[1,∞)
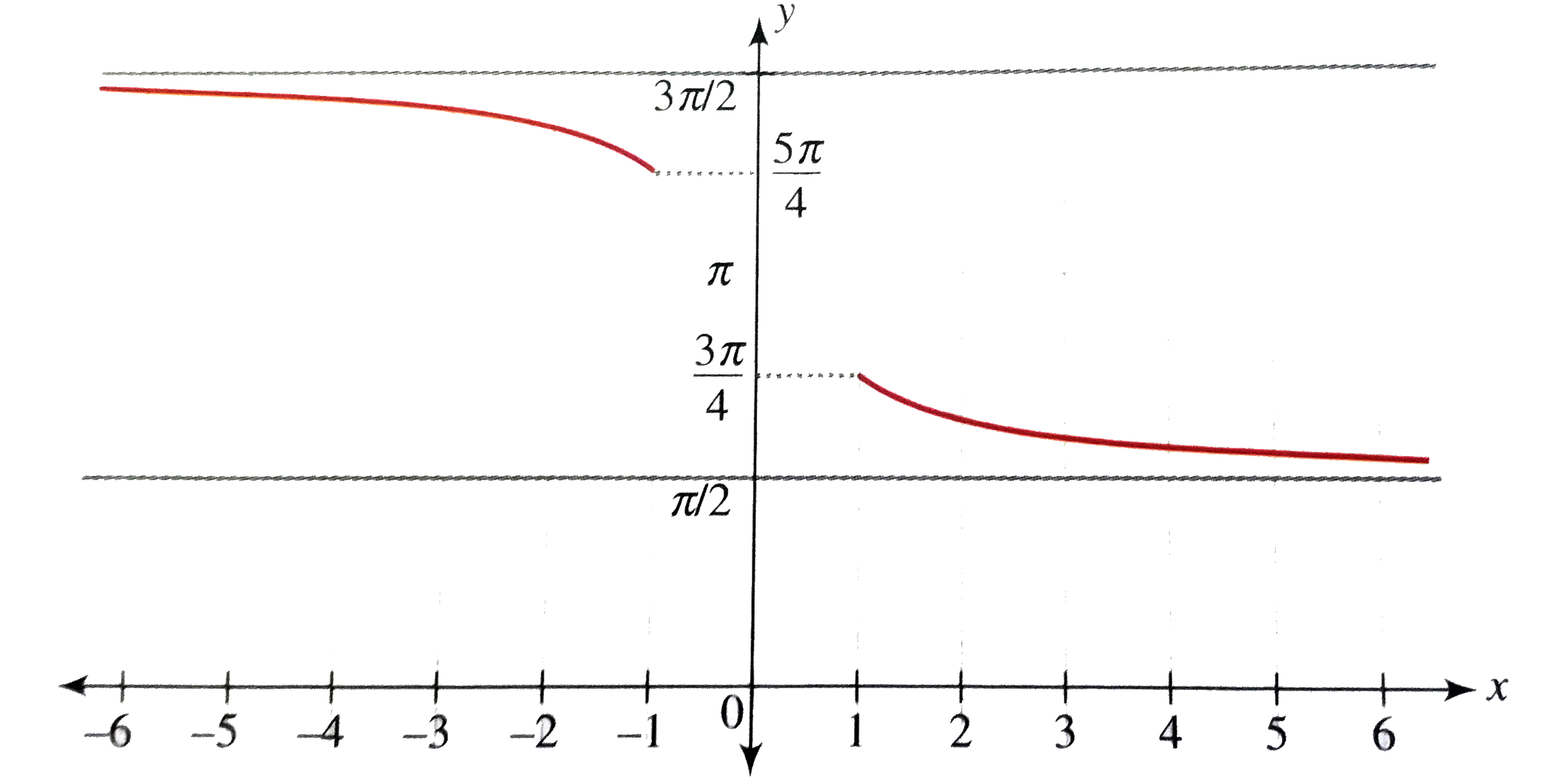
|
Topper's Solved these Questions
- GRAPHICAL TRANSFORMATIONSBOOK - CENGAGECHAPTER - GRAPHICAL TRANSFORMATIONSEXERCISE - Exercise
22 Videos
- GRAPH OF INVERSE TRIGONOMETRIC FUNCTIONSBOOK - CENGAGECHAPTER - GRAPH OF INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise
18 Videos
- GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSBOOK - CENGAGECHAPTER - GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSEXERCISE - Exercise
13 Videos
Similar Questions
Draw the graph of y=cot−1|x|.
View SolutionDraw the graph of y=sec−1x+cosec−1x
View SolutionDraw the graph of y=tan−1x−cot−1x.
View SolutionDraw the graph of y=tan−1x+cot−1x
View SolutionDraw the graph of y=sec−1|x|.
View SolutionDraw the graph of y=cot−1(cotx)
View SolutionDraw the graph of y=sin−1x+cos−1x.
View SolutionDraw the graph of y=x+1x
View SolutionDraw the graph of y=(x−1)(x2−x+1).
View SolutionDraw the graph of y=√xx−1
View Solution
