E and F are points on the sides PQ and PR respectively of ΔPQR. For each of the following cases, state whether EF || QR:
(i) PE = 3.9 cm. EQ = 3 cm. PF = 3.6 cm and FR = 2.4 cm
(ii) PE = 4 cm. QE = 4.5 cm. PF = 8 cm and RF = 9 cm
(iii) PQ = 1.28 cm, PR = 2.56 cm, PE = 0.18 cm and PF = 0.36 cm
(i) As per data,
PE=3.9,EQ=3,PF=3.6andFR=2.4
By basic proportionality theorem,
PEEQ=3.93=1.3
PFFR=3.62.4=1.5
hence, both are not equal,
Thus, EF is not parallel to QR
(ii) As per data,
PE=4,EQ=4.5,PF=8andFR=9
By basic proportionality theorem,
PEEQ=89
PFFR=89
hence, both are equal,
Thus, EF is parallel to QR
(iii) As per data,
PQ=1.28,PR=2.56,PE=0.18andPF=0.36
From EQ=PQ−PE=1.10
FR=PR−PF=2.20
By basic proportionality theorem,
PEEQ=0.181.10=955
PFFR=0.362.20=955
hence, both are equal,
Thus, EF is parallel to QR
Similar Questions
M and N are points on sides AC and BC respectively of a △ABC. State whether MN||BA if CM = 4.2 cm, MA= 2.8 cm , NB = 3.6 cm, CN = 5.7 cm.
View SolutionIn given figure, check whether AD is the bisector of ∠ A of △ ABC in each of the following: (i) AB = 5 cm, AC = 10 cm, BD = 1.5 cm and CD = 3.5 cm (ii) AB = 4 cm, AC = 6 cm, BD = 1.6 cm and CD = 2.4 cm (iii) AB = 8 cm, AC = 24 cm, BD = 6 cm and BC = 24 cm (iv) AB = 6 cm, AC = 8 cm, BD = 1.5 cm and CD = 2 cm (v) AB = 5 cm, AC = 12 cm, BD = 2.5 cm and BC = 9 cm
View SolutionS and T are points on the sides PQ and PR, respectively of ΔPQR, such that PT = 2 cm, TR = 4 cm and ST is parallel to QR. Find the ratio of the areas of ΔPST and ΔPQR.
View SolutionIf P and Q are points on the sides AB and AC respeactively of △ABC, if PQ||BC,l AP= 2 cm , AB = 6 cm and AC= 9 cm find AQ.
View SolutionP and Q are points on the sides AB and AC respectively of a △ABC. If AP= 2cm, PB = 4cm AQ= 3cm and QC= 6cm. Show that BC= 3PQ.
View SolutionIn ΔABC,D and E are the points on sides AB and AC respectively.
Find whether DE || BC, if :
AB = 9 cm, AD = 4 cm, AE = 6 cm and EC = 7.5 cm.View SolutionIn the following figure, ABCD to a trapezium with AB // DC. If AB=9cm,DC=18cm,CF=13.5cm,AP=6cmandBE=15cm
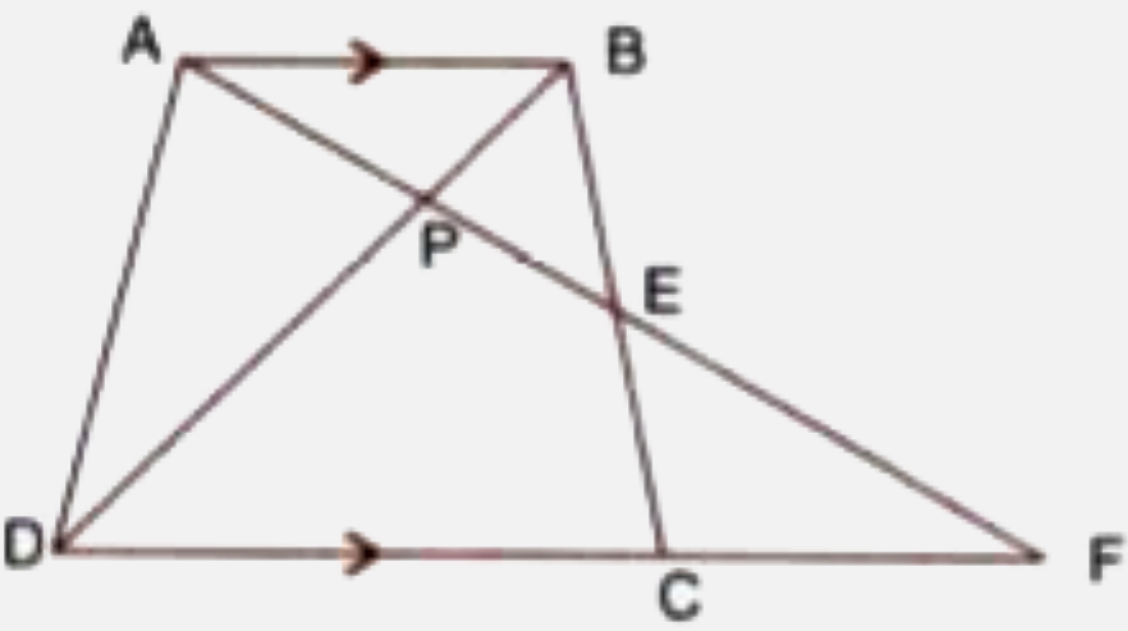
Calculate
PEView SolutionIn ΔABC,D and E are points on the sides AB and AC respectively. Find whether DE||BC if
(i) AD= 3cm , BD = 4.5cm, AE = 4cm, AC= 10cm
(ii) AB=7 cm , BD = 4.5cm, AE = 3.5 cm, CE= 5.6cm.
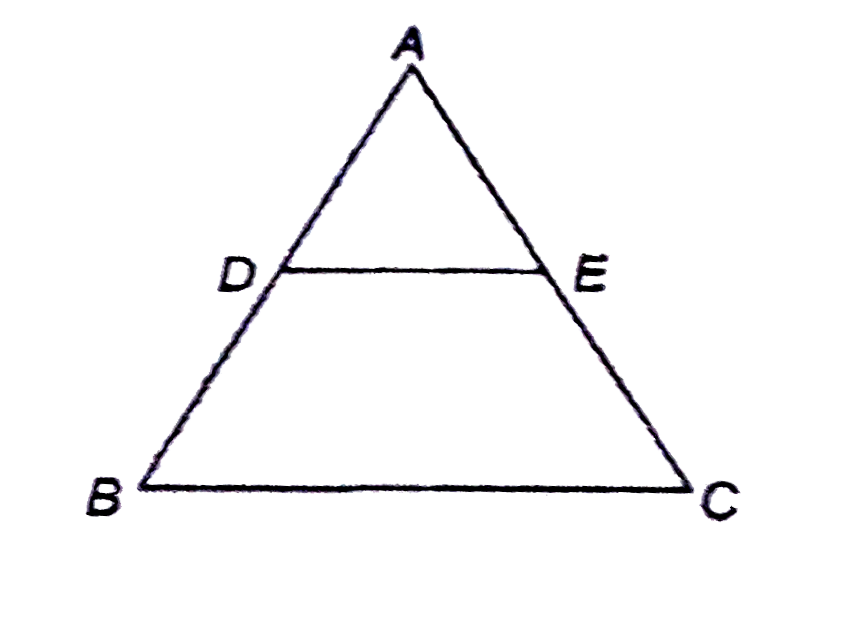 View Solution
View SolutionIn the following figure, XY is parallel to BC,AX=9cm,XB=4.5cmandBC=18cm.
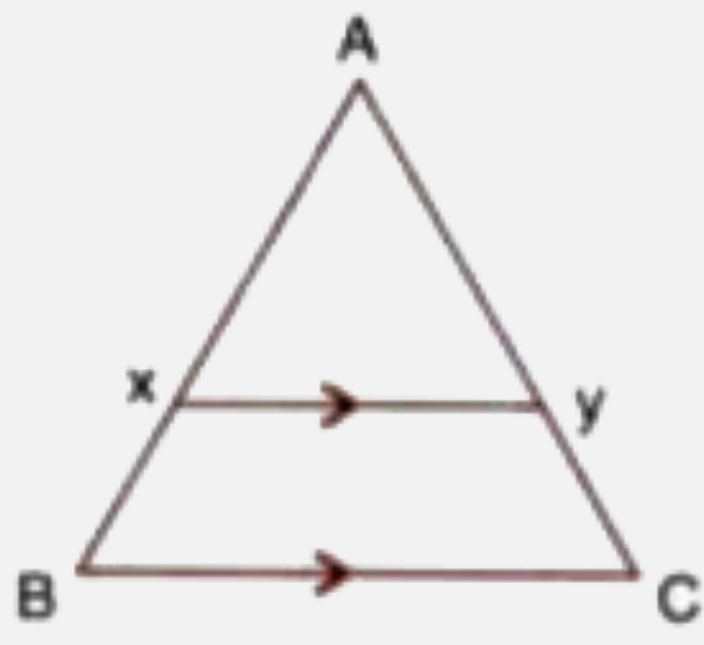
XYView SolutionIn ΔABC, D and E are points on the sides AB and AC respectively. Find whether DE//BC, if :
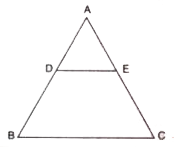
AD=3cm, BD=4.5cm,AE=4cm and AC=10cmView Solution

