E is the mid-point of the median AD of ΔABC. Line segment BE meets AC at point F when produce, prove that AF=13AC.
To prove that AF=13AC given that E is the midpoint of the median AD of triangle ABC and line segment BE meets AC at point F, we can follow these steps:
Step 1: Understand the Triangle and Points
- Let A,B,C be the vertices of triangle ABC.
- Let D be the midpoint of side BC.
- Let E be the midpoint of median AD.
Step 2: Draw Parallel Lines
- Draw a line DG parallel to line segment BE which intersects line AC at point F.
Step 3: Apply the Converse of the Midpoint Theorem in Triangle ADG
- In triangle ADG, since E is the midpoint of AD and EF is parallel to DG, by the Converse of the Midpoint Theorem, we conclude that F is the midpoint of AG.
- Therefore, we can write:
AF=FG
Step 4: Analyze Triangle BCF
- Now, consider triangle BCF. Here, D is the midpoint of BC and BF is parallel to DG.
- Again applying the Converse of the Midpoint Theorem, we find that G is the midpoint of FC.
- Thus, we can write:
FG=GC
Step 5: Relate the Segments
- From the previous steps, we have:
AF=FGandFG=GC
- Therefore, we can conclude:
AF=FG=GC
Step 6: Express AC in Terms of AF
- Since AC can be expressed as:
AC=AF+FG+GC
- Substituting FG and GC with AF:
AC=AF+AF+AF=3AF
Step 7: Solve for AF
- Rearranging the equation gives:
AF=13AC
Conclusion
Thus, we have proven that AF=13AC.
---
- Let A,B,C be the vertices of triangle ABC.
- Let D be the midpoint of side BC.
- Let E be the midpoint of median AD.
- Draw a line DG parallel to line segment BE which intersects line AC at point F.
- In triangle ADG, since E is the midpoint of AD and EF is parallel to DG, by the Converse of the Midpoint Theorem, we conclude that F is the midpoint of AG.
- Therefore, we can write:
AF=FG
- Now, consider triangle BCF. Here, D is the midpoint of BC and BF is parallel to DG.
- Again applying the Converse of the Midpoint Theorem, we find that G is the midpoint of FC.
- Thus, we can write:
FG=GC
- From the previous steps, we have:
AF=FGandFG=GC
- Therefore, we can conclude:
AF=FG=GC
- Since AC can be expressed as:
AC=AF+FG+GC
- Substituting FG and GC with AF:
AC=AF+AF+AF=3AF
- Rearranging the equation gives:
AF=13AC
Thus, we have proven that AF=13AC.
Topper's Solved these Questions
- QUADRILATERALSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - QUADRILATERALSEXERCISE - Revision Exercise (very Short Answer Questions)
10 Videos
- QUADRILATERALSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - QUADRILATERALSEXERCISE - Revision Exercise (short Answer Questions )
10 Videos
- QUADRILATERALSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - QUADRILATERALSEXERCISE - Exercise 8a
29 Videos
- PROBABILITYBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - PROBABILITYEXERCISE - Revision Exercise (very Short Answer /short Answer Questions)
10 Videos
- STATISTICSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - STATISTICSEXERCISE - Revision Exercise
12 Videos
Similar Questions
In parallelogram ABCD, E is the mid-point of AB and AP is parallel to EC which meets DC at point O and BC produced at P. Prove that :
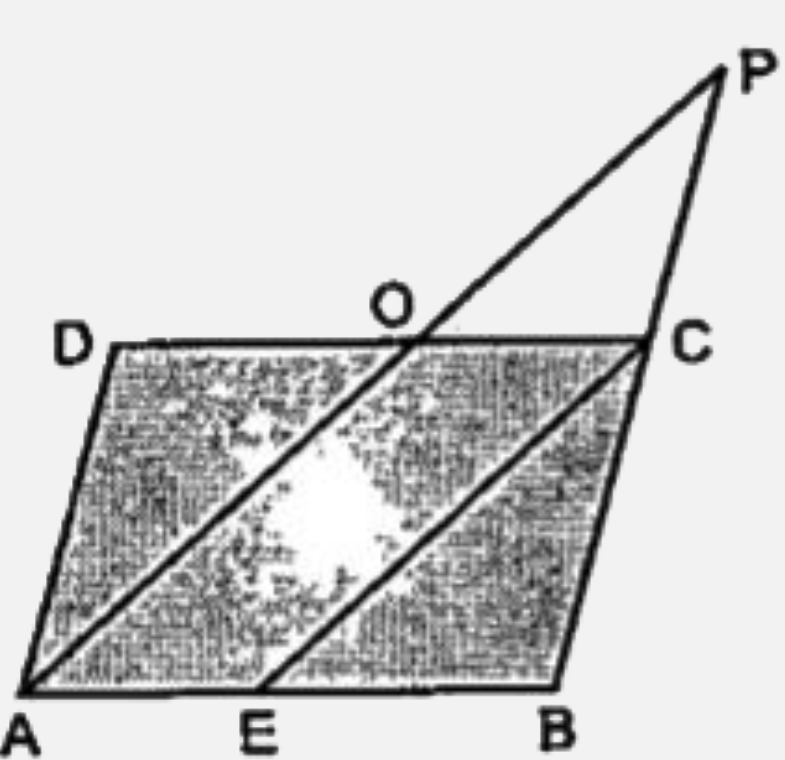
BP=2AD
View SolutionIn parallelogram ABCD, E is the mid-point of AB and AP is parallel to EC which meets DC at point O and BC produced at P. Prove that:
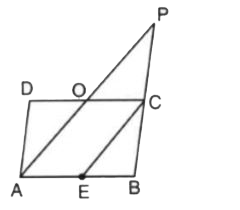
PB=2AD
View SolutionIn a triangle ABC, AD is a median and E is mid-point of median AD. A line through B and E meets AC at point E. Prove that : AC = 3AF Draw DG parallel to BF, which meets AC at point G.
View SolutionThe median AD of the triangle ABC is bisected at E and BE meets AC at F. Find AF:FC.
View SolutionThe median AD of the triangle ABC is bisected at E and BE meets AC at F. Find AF:FC.
View SolutionIn parallelogram ABCD, E is the mid-point of AB and AP is parallel to EC which meets DC at point O and BC produced at P. Prove that:

O is mid-point of AP.
View SolutionD and F are the mid-points of sides AB and AC of a triangle ABC. A line through F and parallel to AB meets BC at point E.
Prove that BDFE is a parallelogram
View SolutionIn A ABC, E is mid-point of the median AD and BE produced meets side AC at point Q. Show that BE : EQ = 3:1.
View SolutionIn figure, P is the mid-point of BC,,Q is the mid-point of AP , such that BQ produced meets AC at R. Prove that 3RA=CA
View SolutionIf D,E and F are the mid-points of the sides BC,CA and AB respectively of the ΔABC and O be any point, then prove that OA+OB+OC=OD+OE+OF
View Solution
