Eleven animals of a circus have to be placed in eleven cages (one in each cage), if 4 of the cages are too small for 6 of the animals, then find the number of the ways of caging all the animals.
Let the 6 animals be placed in 7 of larger cages. This can be done in .7P6 ways. In each of these ways, one larger cage is left vacant. The remaining five animals can be placed in the remaining five cages in 5! Ways. Hence, by the fundamental theorem, the required number of ways is .7P6×5≠604800.
Similar Questions
Eleven animals of a circus have to be placed in eleven cages (one in each cage), if 4 of the cages are too small for 6 of the animals, then find the number of the ways of caging all the animals.
View SolutionIn a circus there are ten cages for accommodating ten animals Out of these four cages are so small that five out of 10 animals cannot enter into them. In how many ways will it is possible to accommodate ten animals in these cages
View Solution
Knowledge Check
Eleven animals of a circus have to be placed in eleven cages (one in each cage), if 4 of the cages are too small for 6 of the animals, then find the number of the ways of caging all the animals.
A7!.5!B4!.6!C6!.6!Dnone of thesem distinct animals of a circus have to be placed in m cages, one in cach cage. If n (< m) cages are too small to accommodate p (n < p < m) animals, then the number of ways of putting the animals into cages are
A(m−nPp)m−nPm−pBm−nCpC(m−nCp)(m−pCm−p)DNone of theseIn a certain zoo, there are 42 animals in one sector, 34 in the second sector and 20 in the third sector. Out ofthis, 24 graze in sector one and also in sector two. 10 graze in sector two and sector three. 12 graze in sector one and sector three. These figures also include four animals grazing in all the three sectors. If all these animals are now transported to another zoo, then find the total number of animals?
A38B56C54DNone of these
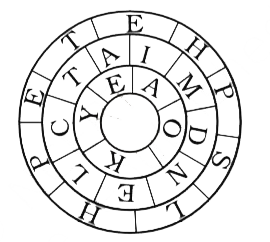
Figure 3.1 shows three rings of circles with letters in them. Some of these letters in each ring can from the name of one wool yielding animal. Find the names of these animals.
View SolutionDo you agree that wild animals should be caged Comment yes or no giving reasons.
View SolutionA small metallic sphere is suspended by a light spring of force constant k from the ceilling of a cage, which is accelerating uniformly by a force F in the upward direction. The ratio of mass of the cage to that of the sphere is 'n'. Find the potential energy stored in the spring.
View SolutionRead the following paragraph carefully and answer the question given.
In a zoological park 5 animals were placed in cages in a row.
The cage of 'Tiger' is to the left of 'Lion' and to the right of Cheetah'. The cage of 'Python' is to the right of 'Lion'. The cage of Puma' is between 'Lion' and 'Python'.
Which animal is immediate left to Puma' ?
View SolutionA small metallic sphere is suspended by a light spring of force constant k from the ceilling of a cage, which is accelerating uniformly by a force F in the upward direction. The ratio of mass of the cage to that of the sphere is 'n'. Find the potential energy stored in the spring.
View Solution
