evaluate limn→∞(enπ)1nSolution in Punjabi
The correct Answer is:=e
Step by step video & image solution for evaluate lim_(n->oo)((e^n)/pi)^(1/ n) by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- LIMITSBOOK - ARIHANT MATHSCHAPTER - LIMITSEXERCISE - SOLVED EXAMPLES
1 Videos
- LIMITSBOOK - ARIHANT MATHSCHAPTER - LIMITSEXERCISE - Exercise (Single Option Correct Type Questions)
38 Videos
- INVERSE TRIGONOMETRIC FUNCTIONSBOOK - ARIHANT MATHSCHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
8 Videos
- LOGARITHM AND THEIR PROPERTIESBOOK - ARIHANT MATHSCHAPTER - LOGARITHM AND THEIR PROPERTIESEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
4 Videos
Similar Questions
To evaluate limx→a[f(x)], we must analyse the f(x) in right hand neighbourhood as well as in left hand neighbourhood of x=a. E.g. In case of continuous function, we may come across followign cases.
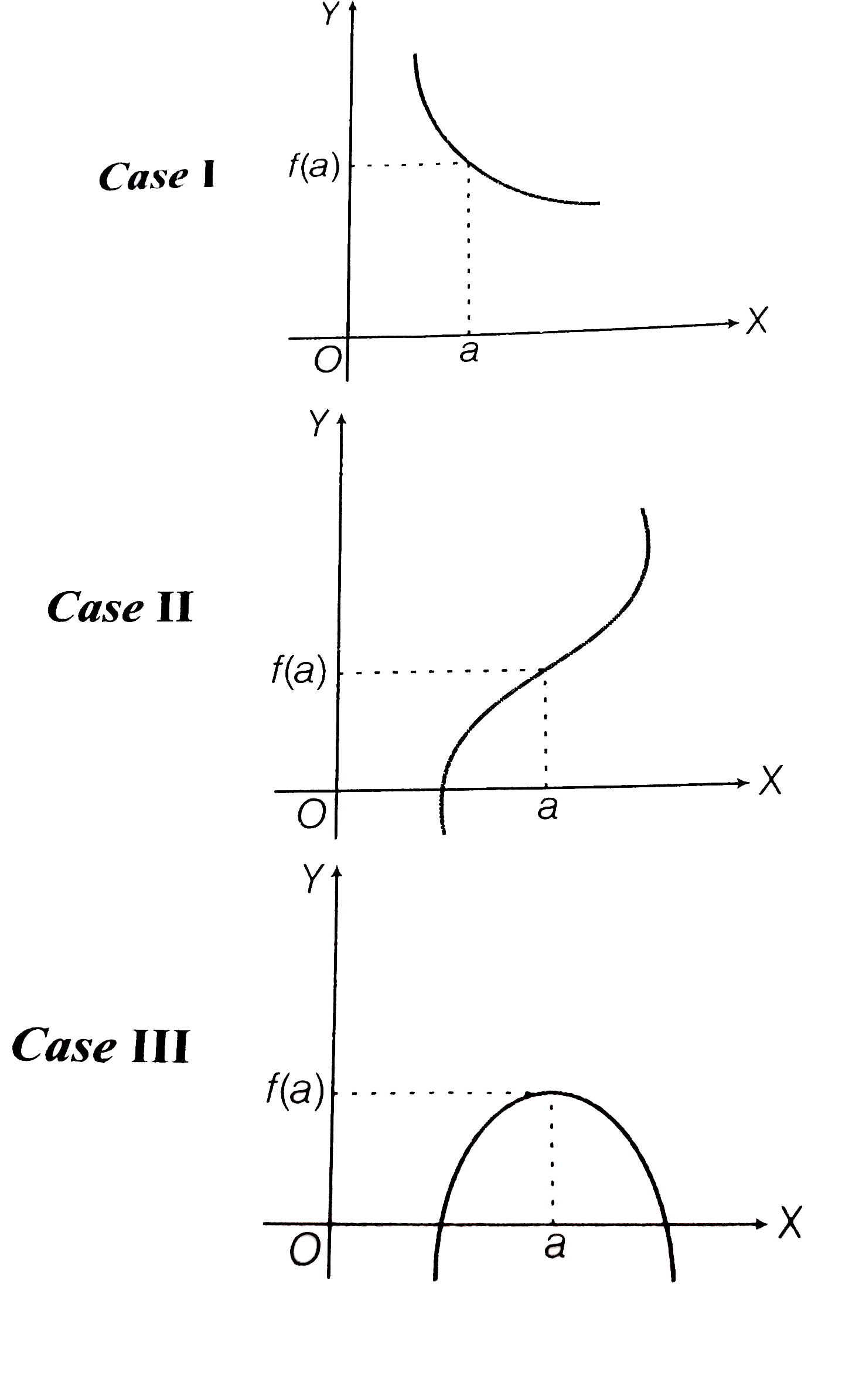
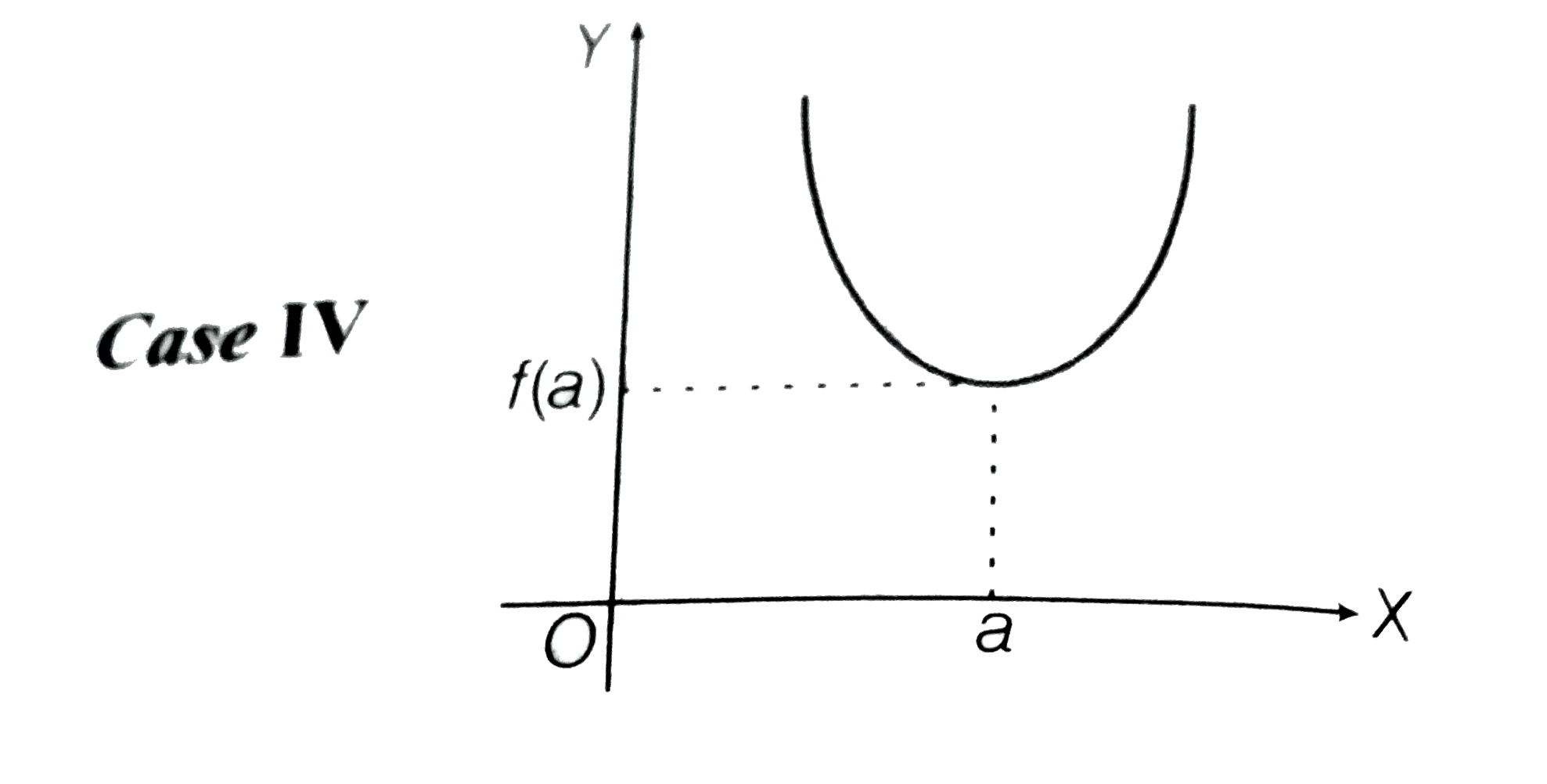
Iff(a) is an integer, the limit will exist in Case III and Case IV but not in Case I and Case II. If f(a) is not an integer, the limit exists in all the cases. ltbgt If f'(1)=−3 and limx→1[f(x)−12] does not exist, (where [.] denotes the greatest integer function), then
View Solutionlimx→0sin(πcos2(tan(sinx)))x2 is equal to
View SolutionIf α=3sin−1(611andβ=3cos−1(49), where the inverse trigonometric functions take only the principal values, then the correct options (s) is (are)
View SolutionIn Which quadrant Point (−2,−3) will be lie.
View SolutionEvaluate: (lim)x→∞sinn(2πn3n+1),n∈N.
View SolutionThe value of lim_ (n rarr oo) [(1) / (n) + (e ^ ((1) / (n))) / (n) + (e ^ ((2) / (n))) / (n) + .... + (e ^ ((n-1) / (n))) / (n)] is:
View SolutionFind lim_ (n rarr oo) [n ^ (n) * (n + 1)! -: [n! (N + 1) ^ (n + 1)]
View SolutionFind lim_ (n rarr oo) n ^ (n) (1 + n) ^ (- n)
View SolutionFind lim_ (n rarr oo) [(n + 1) ^ (n + 1) * n ^ (- n-1) - (n + 1) * n ^ (- 1)]
View Solutionevaluate lim_ (n rarr oo) ((e ^ (n)) / (pi)) ^ ((1) / (n))
View Solutionlim_ (n rarr oo) [(e ^ (1 / n) + e ^ (2 / n) + e ^ (3 / n) + ... + e ^ (n / n)) / (n)]
View Solutionlim_ (n rarr oo) [(e ^ ((1) / (n)) + e ^ ((2) / (n)) + e ^ ((3) / (n)) ++ e ^ ((n ) / (n))) / (n)]
View Solutionlim_ (n rarr oo) [(e ^ (1 / n) + e ^ (2 / n) + e ^ (3 / n) + ... + e ^ (n / n)) / (n)]
View SolutionIf A=[1a01] then find limn−∞1nAn
View Solutionlimx→∞1n{1+e1/n+e2/n+e3/n+.....+en−1n} is equal to
View SolutionEvaluate limn→∞[(1+1n)(1+2n)⋅⋅⋅(1+nn)]1n
View Solution
