Evaluate the following: ∣∣ ∣ ∣∣ahghbfgfc∣∣ ∣ ∣∣
To evaluate the determinant of the matrix
∣∣
∣∣ahghbfgfc∣∣
∣∣
we will use the method of cofactor expansion along the first row.
1. Define the Determinant:
Let D=∣∣
∣∣ahghbfgfc∣∣
∣∣.
2. Expand along the first row:
Using cofactor expansion along the first row, we have:
D=a∣∣∣bffc∣∣∣−h∣∣∣hfgc∣∣∣+g∣∣∣hbgf∣∣∣
3. Calculate the 2x2 Determinants:
- For the first determinant:
∣∣∣bffc∣∣∣=bc−f2
- For the second determinant:
∣∣∣hfgc∣∣∣=hc−fg
- For the third determinant:
∣∣∣hbgf∣∣∣=hf−bg
4. Substituting Back:
Now substitute these values back into the equation for D:
D=a(bc−f2)−h(hc−fg)+g(hf−bg)
5. Distributing Terms:
Expanding this gives:
D=abc−af2−h2c+hfg+ghf−g2b
6. Combine Like Terms:
Rearranging the terms, we get:
D=abc−af2−h2c+2hfg−g2b
Final Answer:
Thus, the determinant evaluates to:
D=abc−af2−h2c+2hfg−g2b
∣∣ahghbfgfc∣∣
∣∣
Let D=∣∣
∣∣ahghbfgfc∣∣
∣∣.
Using cofactor expansion along the first row, we have:
D=a∣∣∣bffc∣∣∣−h∣∣∣hfgc∣∣∣+g∣∣∣hbgf∣∣∣
- For the first determinant:
∣∣∣bffc∣∣∣=bc−f2
- For the second determinant:
∣∣∣hfgc∣∣∣=hc−fg
- For the third determinant:
∣∣∣hbgf∣∣∣=hf−bg
Now substitute these values back into the equation for D:
D=a(bc−f2)−h(hc−fg)+g(hf−bg)
Expanding this gives:
D=abc−af2−h2c+hfg+ghf−g2b
Rearranging the terms, we get:
D=abc−af2−h2c+2hfg−g2b
Thus, the determinant evaluates to:
D=abc−af2−h2c+2hfg−g2b
Similar Questions
If A,B,C are matrices such that A=[xyz],B=⎡⎢⎣ahghbfgfc⎤⎥⎦ and C=⎡⎢⎣xyz⎤⎥⎦ then find ABC
View SolutionWhat is the order of the product [x y z]⎡⎢⎣ahghbfgfc⎤⎥⎦⎡⎢⎣xyz⎤⎥⎦?
View SolutionIf U={a,b,c,d,e,f,g,h}, find the complements of the following sets :(i) A={a,b,c} (ii) B={d,e,f,g] (iii) C={a,c,e,g} (iv) D={f,g,h,a)
View SolutionIf U={a,b,c,d,e,f,g,h}, find the complements of the following sets :(i) A={a,b,c} (ii) B={d,e,f,g] (iii) C={a,c,e,g} (iv) D={f,g,h,a)
View SolutionCalculate heat of the following reaction at constant pressure,
F2O(g)+H2O(g)→O2(g)+2HF(g)
The heats of formation of F2O(g),H2O(g) and HF(g) are 5.5kcal−57kcal and −64kcal repectively.
View SolutionIf A=[xyz],B=⎡⎢⎣ahghbfgfc⎤⎥⎦,C=[αβγ]T then ABC is
View SolutionIf f,g, and h are differentiable functions of x and (δ)=∣∣ ∣ ∣∣fgh(xf)'(xg)'(xh)'(x2f)''(x2g)''(x2h)''∣∣ ∣ ∣∣ prove that δ′=∣∣ ∣ ∣∣fghf'g'h(x3f'')'(x3g'')'(x3h'')'∣∣ ∣ ∣∣
View SolutionGraph of y=f(x)andy=g(x) is given in the following figure. If h(x)=f(g(x)), then find the value of h'(2).
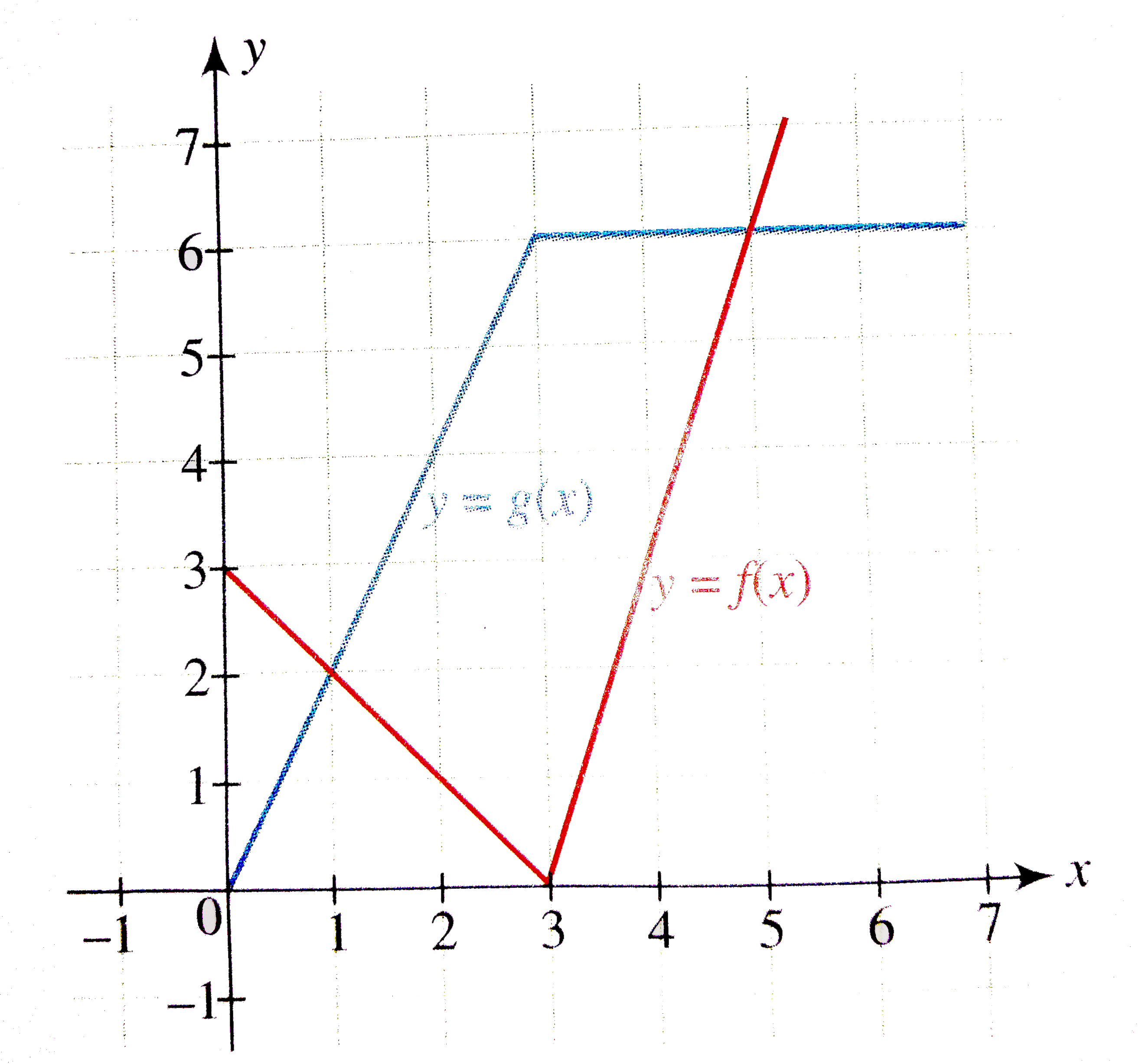
View SolutionUsing the given diagram, express the following sets in terms of set A and B.

(i) {a,d} , (ii) {a,d,c,f}, (iii) {a,d,c,f,g,h}, (iv) {a,d,g,h}, (v) {g,h}
View SolutionThe standard enthalpy change for the following reaction is 436.4 kJ :
H2(g)→H(g)+H(g)
What is the ΔfH∘ of atomic hydrogen (H)?
View Solution
