Evaluate limx−2xn−2nx−2Solution in Tamil
The correct Answer is:32
Step by step video, text & image solution for Evaluate underset(x -2)(lim) (x^(n)- 2^(n))/(x-2) by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- DIFFERENTIAL CALCULUS LIMITS AND CONTINUITYBOOK - PREMIERS PUBLISHERSCHAPTER - DIFFERENTIAL CALCULUS LIMITS AND CONTINUITYEXERCISE - SOLUTION TO EXERCISE 9.1
24 Videos
- DIFFERENTIAL CALCULUS LIMITS AND CONTINUITYBOOK - PREMIERS PUBLISHERSCHAPTER - DIFFERENTIAL CALCULUS LIMITS AND CONTINUITYEXERCISE - SOLUTION TO EXERCISE 9.2
15 Videos
- DIFFEREMTIAL CALCULUS DIFFERENTIABILITY AND METHODS OF DIFFERENTITAION BOOK - PREMIERS PUBLISHERSCHAPTER - DIFFEREMTIAL CALCULUS DIFFERENTIABILITY AND METHODS OF DIFFERENTITAION EXERCISE - PROBLEMS FOR PRACTICE
73 Videos
- EXAMINATION QUESTION PAPER MARCH 2019BOOK - PREMIERS PUBLISHERSCHAPTER - EXAMINATION QUESTION PAPER MARCH 2019EXERCISE - PART -IV
4 Videos
Similar Questions
Complete the table using calculator and use the result to estimate the limit.
1 limx→2x−2x2−x−2
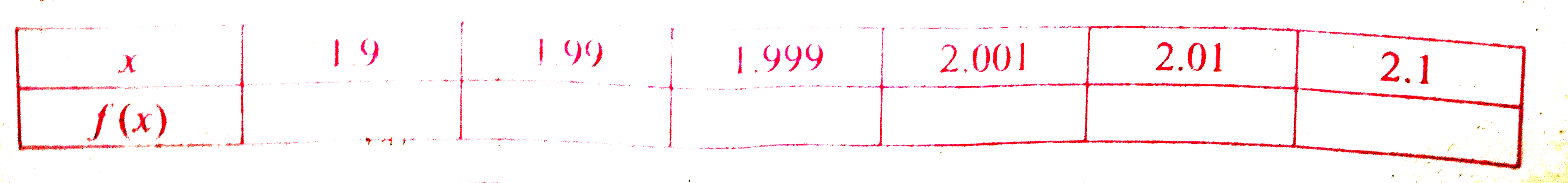
View SolutionSolve : limx→2x4−16x−2
View SolutionIfy=13√x+log5x+8,f∈ddydx.
View SolutionWrite any five different forms of an equation of a straight line.
View SolutionFind (i) lim6x→5
(ii) limxx→2
(iii)lim[x+2]x→3
(iv) lim4x+2x→2)
View Solution(i) Let h(x)=limx→∞x2nf(x)+g(x)1+x2n, find h(x) in terms of f(fx) and g(x)
(ii) without using L Hospital rule or series expansion for exevaluate limx→0ex−1−xx2
(iii) limn→∞⎡⎢ ⎢ ⎢⎣e1nn2+2(e1n)2n2+3.(e1n)3n2+.......+n(e1n)nn2⎤⎥ ⎥ ⎥⎦
(iv) limx→0[asinxx]+[btanxx] Where a,b are inegers and [] denotes integral part.
(v) limx→a(sinxsina)1x−a
View Solutionlimn→∞1n3n∑k=1[k2x]=
View Solutionlimx→0(cosmx)n/x2
View SolutionIf limx→0(sinnx)[(a−n)nx−2tanx]x2=0 then value of a=
View Solutionlimx→1x+x2+x3+.....+xn−nx−1 =
View SolutionShow : limx→2(1+x)n−3nx−2=n.3n−1
View SolutionStatement -I : limx→∞(12x3+22x3+32x3+......+x2x3)=limx→∞12x3+limx→∞22x3+....+limx→∞x2x3=0
Statement - II : limx→a{f1(x)+f2(x)+....+fn(x)}=limx→af1(x)+limx→af2(x)+...+limx→afn(x)
View SolutionEvaluate limx−2xn−2nx−2
View SolutionIf [x] denotes the greatest integer ≤x, then limn→∞1n3{[12x]+[22x]+[32x]+...+[n2x]}=
View SolutionEvaluate : limx→1(x+x2+x3+……….+xn)−nx−1
View SolutionIf limx→0(sinnx)[(a−n)nx−tanx]x2=0, then the value of a.
View Solution
