Every proression is a sequence but the converse i.e., every sequence is also a progression need not mecessarily be true.
To solve the question, we need to analyze the statements regarding sequences and progressions. Let's break it down step by step.
Step 1: Understanding Progressions and Sequences
- A sequence is an ordered list of numbers, which can follow a specific rule or pattern.
- A progression is a specific type of sequence where the numbers follow a defined pattern. The two most common types of progressions are:
- Arithmetic Progression (AP): A sequence where the difference between consecutive terms is constant.
- Geometric Progression (GP): A sequence where the ratio between consecutive terms is constant.
Step 2: Justifying the First Statement
- The first statement claims that "every progression is a sequence."
- To justify this, we can take an example of an arithmetic progression:
- Consider the sequence: 2, 4, 6, 8, ...
- This is an arithmetic progression where the common difference (d) is 2.
- Since this sequence follows a specific rule (adding 2 each time), it is indeed a sequence.
Step 3: Analyzing the Second Statement
- The second statement claims that "every sequence is also a progression."
- To analyze this, we can take an example of a sequence that is not a progression:
- Consider the sequence of prime numbers: 2, 3, 5, 7, 11, 13, ...
- In this sequence, the differences between consecutive terms are not constant:
- The differences are: 1 (3-2), 2 (5-3), 2 (7-5), 4 (11-7), 2 (13-11).
- Since there is no fixed pattern in the differences, this sequence does not qualify as a progression.
Step 4: Conclusion
- Therefore, the first statement is true: every progression is a sequence.
- The second statement is false: not every sequence is a progression, as demonstrated by the sequence of prime numbers.
Final Answer
In conclusion, while every progression is indeed a sequence, the converse is not necessarily true, as shown by the example of the sequence of prime numbers.
---
- A sequence is an ordered list of numbers, which can follow a specific rule or pattern.
- A progression is a specific type of sequence where the numbers follow a defined pattern. The two most common types of progressions are:
- Arithmetic Progression (AP): A sequence where the difference between consecutive terms is constant.
- Geometric Progression (GP): A sequence where the ratio between consecutive terms is constant.
- The first statement claims that "every progression is a sequence."
- To justify this, we can take an example of an arithmetic progression:
- Consider the sequence: 2, 4, 6, 8, ...
- This is an arithmetic progression where the common difference (d) is 2.
- Since this sequence follows a specific rule (adding 2 each time), it is indeed a sequence.
- The second statement claims that "every sequence is also a progression."
- To analyze this, we can take an example of a sequence that is not a progression:
- Consider the sequence of prime numbers: 2, 3, 5, 7, 11, 13, ...
- In this sequence, the differences between consecutive terms are not constant:
- The differences are: 1 (3-2), 2 (5-3), 2 (7-5), 4 (11-7), 2 (13-11).
- Since there is no fixed pattern in the differences, this sequence does not qualify as a progression.
- Therefore, the first statement is true: every progression is a sequence.
- The second statement is false: not every sequence is a progression, as demonstrated by the sequence of prime numbers.
In conclusion, while every progression is indeed a sequence, the converse is not necessarily true, as shown by the example of the sequence of prime numbers.
Topper's Solved these Questions
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - SEQUENCE AND SERIESEXERCISE - Match the comumms2videos
SEQUENCE AND SERIES
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - SEQUENCE AND SERIESEXERCISE - Fillers3videos
SEQUENCE AND SERIES
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - RELATIONS AND FUNCTIONS EXERCISE - True /False5videos
RELATIONS AND FUNCTIONS
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - SETSEXERCISE - TRUE AND FALSE6videos
SETS
Similar Questions
The correct sequence of reagents for the following conversion is
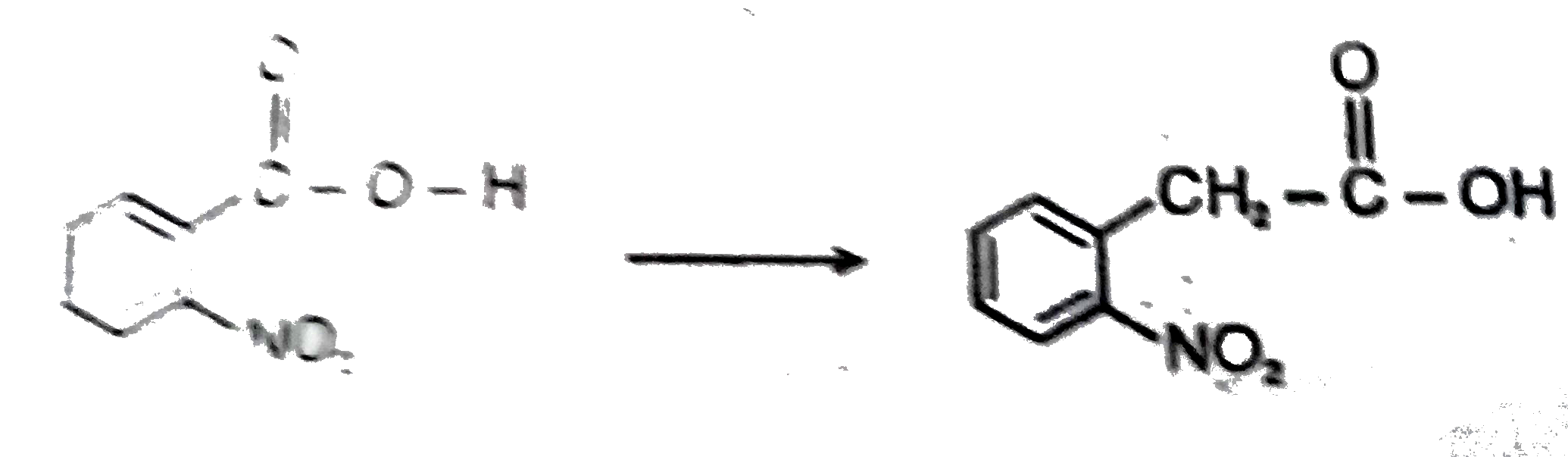 View Solution
View SolutionThe best sequence of reactions for the following conversion is
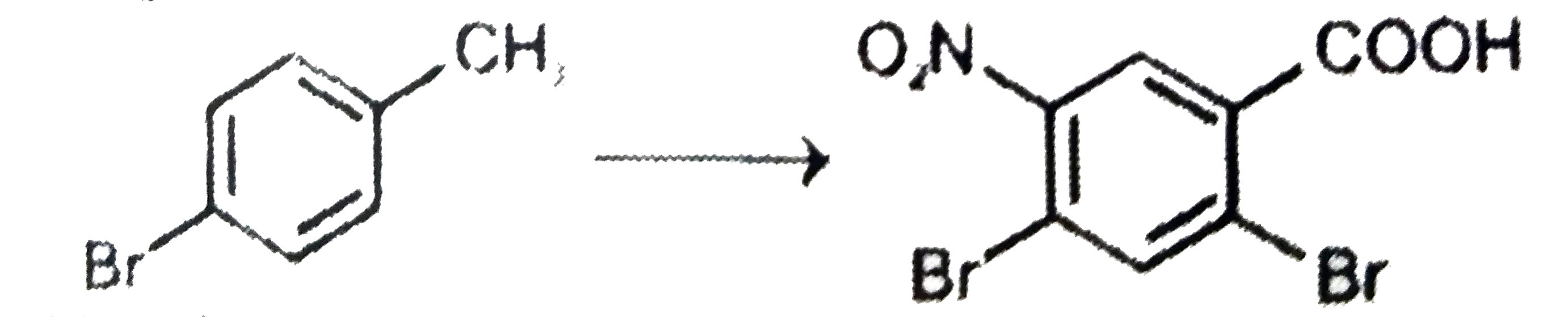 View Solution
View SolutionStages in proper sequence of prophase I are
View SolutionProve that every identity relation on a set is reflexive, but the converse is not necessarily true.
View SolutionProve that every identity relation on a set is reflexive, but the converse is not necessarily true.
View SolutionProve that every identity relation on a set is reflexive, but the converse is not necessarily true.
View SolutionThe graph of every linear equation in two variables need not be a line.
View SolutionThe first term of a sequence is 1, the second is 2 and every term is the sum of the two preceding terms.The nth term is.
View SolutionLet {a1,a2,a3......} be a strictly increasing sequence of positive integers in an arithmetic progression. Prove that there is an infinite subsequence of the given sequence whose terms are in a geometric progression.
View Solution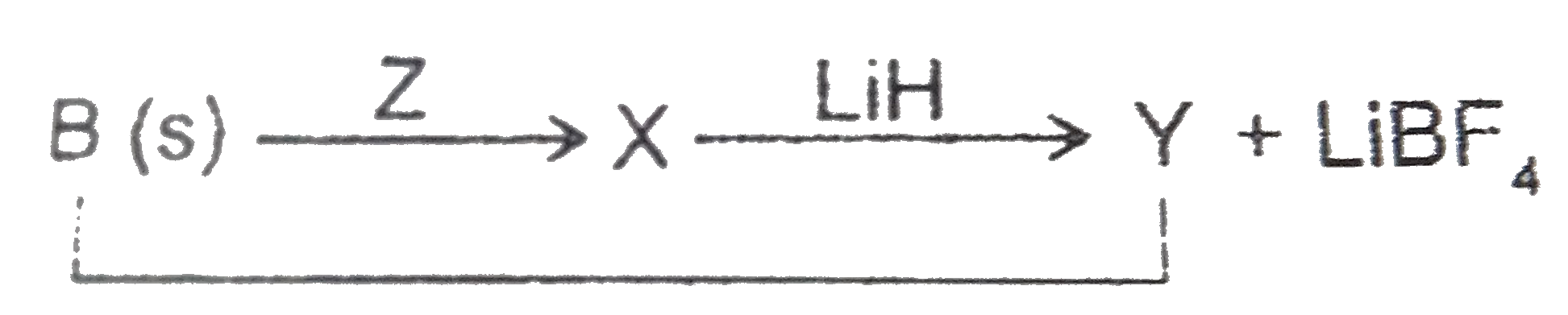
Which of the statement is true for the above sequence of reactions?View Solution

