Examine the applicability of Mean Value Theorem for all three functions given in the above exercise 2.
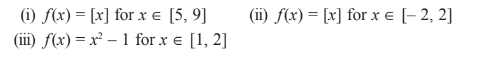
(i) As the function f(x)=[x] is neither continuous nor derivable , conditions of mean value theorem is not satisfied hence not verified .
(ii) Given function is,
f(x)=[x],x∈[−2,2]
From the above equation (1), it is clear that the function f(x) is not continuous at x=−2andx=2.
The value of function at point −2 is,
f(−2)=[−2]=−2
The value of function at point 2 is,
f(2)=[2]=2
It can be observed that f(−2)inf(2).
The differentiability of the function can be check as follows. Let, b is an integer.
The left hand limit of fat x=bis,
limh→0f(b+h)−f(b)h=limh→0[b+h]−[b]h=limh→0b−1−bh=limh→0−−1h=∞
The right hand limit of f at x=b is,
limh→0f(b+h)−f(b)h=limh→0[b+h]−[b]h=limh→0b−bh=0
Since, right hand limit is not equal to the left hand limit therefore function is not differentiable in the given interval.
Therefore, Mean value theorem is not satisfied for the given function f(x)=[x] for x∈[−2,2].
(iii)Given function is,
f(x)=x2−1,x∈[1,2]
The first derivative of the function f'(c)=0 for some value, where c∈(a,b).
From the above equation (1), it is clear that the function f(x) is continuous at x=1andx=2.
The value of function at point 1 is,
f(1)=(1)2−1=0
The value of function at point 2 is,
f(2)=(2)2−1=3
It can be observed that f(1)∈f(2).
The differentiability of the function can be check as follows. Let, b is an integer.
The left hand limit of the function at x=b is,
limh→0(f(b+h)−fb))h=limh→0{(b+h)2−1}−{b2−1}h=limh→0{b2+2bh+h2−1}−(b2+1)h=limh→02bhh=2b
The right hand limit of fat x=b is,
limh→0f(b+h)−f(b)h=limh→0{(b+h)2−1}−{b2−1}h=limh→02bhh=2b
Since, right hand limit is equal to the left hand limit therefore function is differentiable in the given interval.
Therefore, Mean value theorem is satisfied for the given function f(x)=x2−1 for x∈[1,2].
Topper's Solved these Questions
- BOOK - NCERTCHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - EXERCISE 5.518videos
CONTINUITY AND DIFFERENTIABILITY
- BOOK - NCERTCHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - EXERCISE 5.717videos
CONTINUITY AND DIFFERENTIABILITY
- BOOK - NCERTCHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - EXERCISE 5.315videos
CONTINUITY AND DIFFERENTIABILITY
- BOOK - NCERTCHAPTER - APPLICATION OF INTEGRALSEXERCISE - EXERCISE 8.27videos
APPLICATION OF INTEGRALS
- BOOK - NCERTCHAPTER - DETERMINANTSEXERCISE - EXERCISE 4.45videos
DETERMINANTS
Similar Questions
Knowledge Check
- Question 1 - Select One
The value of c in mean value theorem for the function f(x)=x2 in [2,4] is
A3B2C4D72
Examine the validity of Lagrange's mean value theorem for the function f(x)=x2/3 in the interval [−1,1].
View SolutionExamine the validity of Lagrange's mean value theorem for the function f(x)=x2/3 in the interval [−1,1].
View SolutionDiscuss the applicability of Lagranges mean value theorem for the function f(x)=|x| on [−1, 1] .
View SolutionDiscuss the applicability the Rolle's theorem for the function f(x) = x2 in the interval [2,3].
View SolutionVerify Lagrange's Mean Value Theorem for the functions :
f(x)=x on [a,b]View SolutionVerify the Mean Value Theorm for f(x)=x2 in the interval [2,4].
View SolutionVerify Lagrange's Mean Value Theorem for the functions :
f(x)=logex in the interval [1, 2]View Solution

