Examples :- If x;y∈{1;2;3;4};then which of the following are function in the given set ? (a) f_1={(x;y):y=(x+1)} (b) f_2={(x;y):y4 (d) f_4={(x;y):x+y=5}
To determine which of the given sets are functions, we need to analyze each option based on the definition of a function. A relation f from a set X to a set Y is a function if every element in X is associated with exactly one element in Y.
Given the sets X={1,2,3,4} and Y={1,2,3,4}, we will evaluate each option.
1. Evaluate f1={(x,y):y=(x+1)}:
- For x=1, y=2
- For x=2, y=3
- For x=3, y=4
- For x=4, y=5 (not in set Y)
- Since y must be in Y and y=5 is not in Y, f1 is not a function.
2. Evaluate f2={(x,y):y<x}:
- For x=1, there are no y values since y<1 is not possible.
- For x=2, y can be 1.
- For x=3, y can be 1,2.
- For x=4, y can be 1,2,3.
- Since x=3 and x=4 can map to multiple y values, f2 is not a function.
3. Evaluate f3={(x,y):x+y>4}:
- For x=1, y can be 4 (only).
- For x=2, y can be 3,4.
- For x=3, y can be 2,3,4.
- For x=4, y can be 1,2,3,4.
- Again, since multiple y values can correspond to the same x, f3 is not a function.
4. Evaluate f4={(x,y):x+y=5}:
- For x=1, y=4.
- For x=2, y=3.
- For x=3, y=2.
- For x=4, y=1.
- Each x value corresponds to exactly one y value, and all pairs are valid. Thus, f4 is a function.
Summary of Results:
- f1: Not a function.
- f2: Not a function.
- f3: Not a function.
- f4: Is a function.
Final Answer:
The only function among the given options is f4.
- For x=1, y=2
- For x=2, y=3
- For x=3, y=4
- For x=4, y=5 (not in set Y)
- Since y must be in Y and y=5 is not in Y, f1 is not a function.
- For x=1, there are no y values since y<1 is not possible.
- For x=2, y can be 1.
- For x=3, y can be 1,2.
- For x=4, y can be 1,2,3.
- Since x=3 and x=4 can map to multiple y values, f2 is not a function.
- For x=1, y can be 4 (only).
- For x=2, y can be 3,4.
- For x=3, y can be 2,3,4.
- For x=4, y can be 1,2,3,4.
- Again, since multiple y values can correspond to the same x, f3 is not a function.
- For x=1, y=4.
- For x=2, y=3.
- For x=3, y=2.
- For x=4, y=1.
- Each x value corresponds to exactly one y value, and all pairs are valid. Thus, f4 is a function.
- f1: Not a function.
- f2: Not a function.
- f3: Not a function.
- f4: Is a function.
The only function among the given options is f4.
Topper's Solved these Questions
Similar Questions
Examples :- If x;y∈{1;2;3;4};then which of the following are function in the given set ? (a) f_1={(x;y):y=(x+1)} (b) f_2={(x;y):y4 (d) f_4={(x;y):x+y=5}
View SolutionWhich of the following functions have the graph symmetrical about the origin? (a) f(x) given by f(x)+f(y)=f(x+y1−xy) (b) f(x) given by f(x)+f(y)=f(x√1−y2+y√1−x2) (c) f(x) given by f(x+y)=f(x)+f(y)∀x,y∈R (d) none of these
View Solution
Knowledge Check
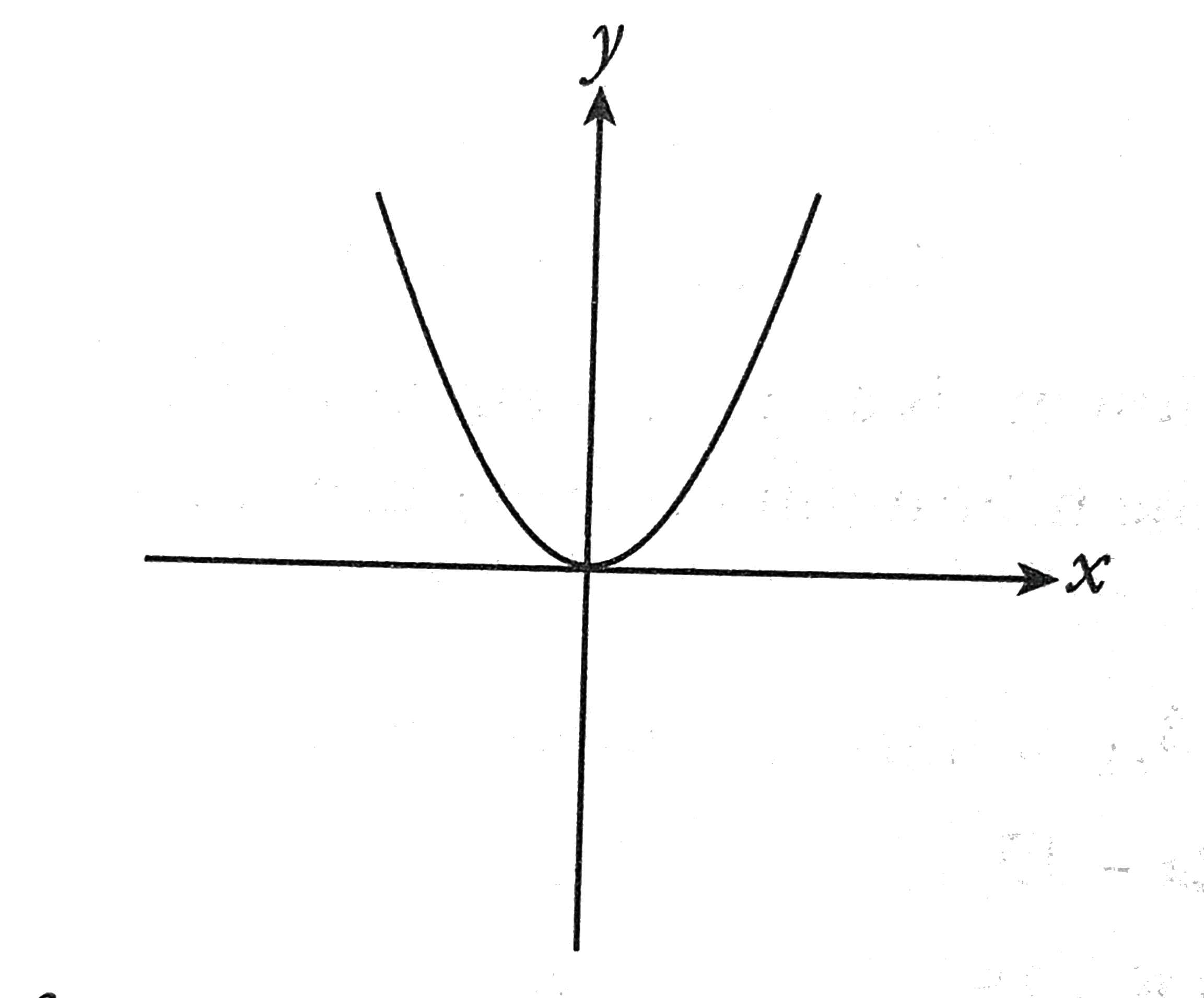
The quadratic y=f(x) is shown above. Which of the following graphs represents the function y=f(x+3)−4?A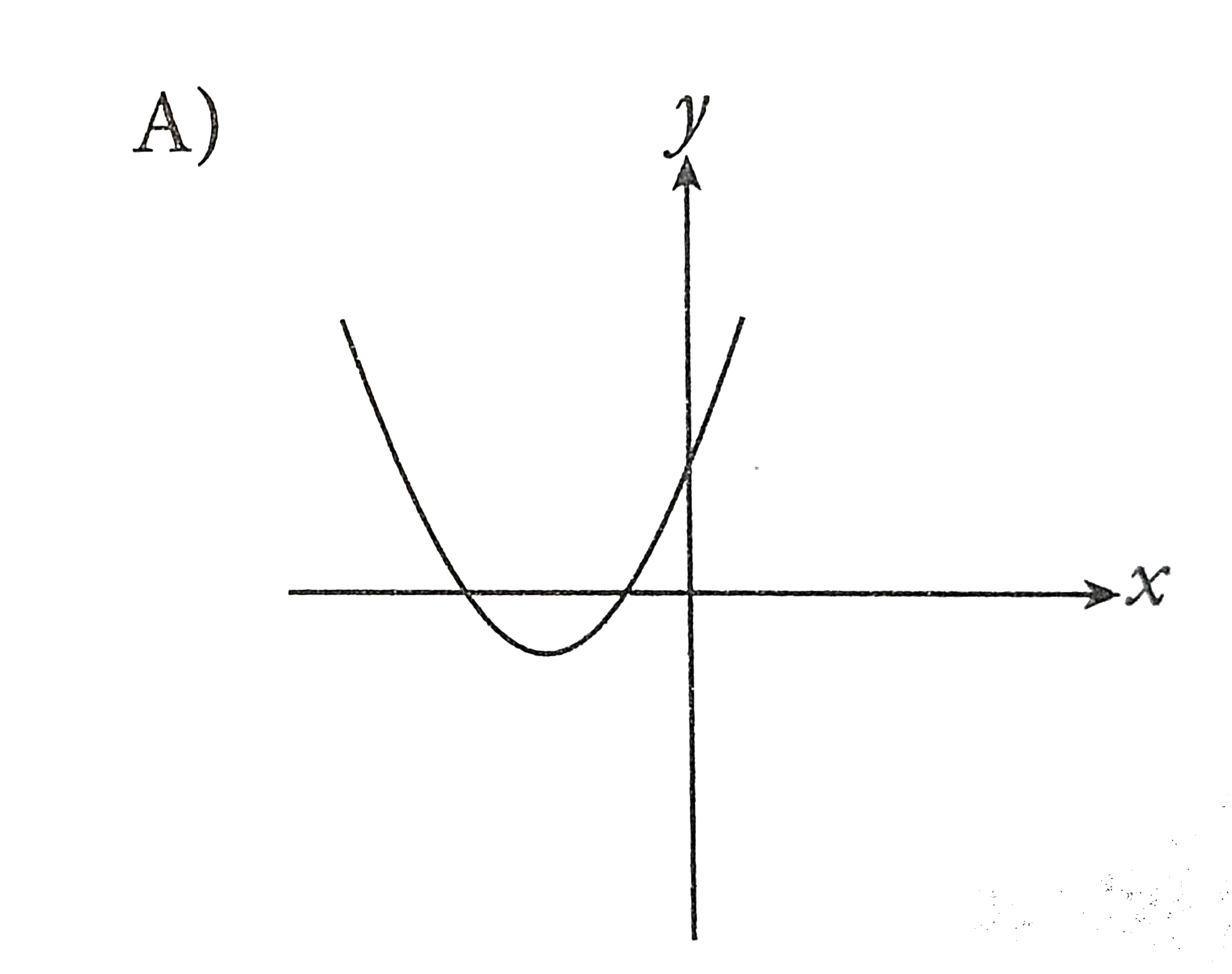 B
B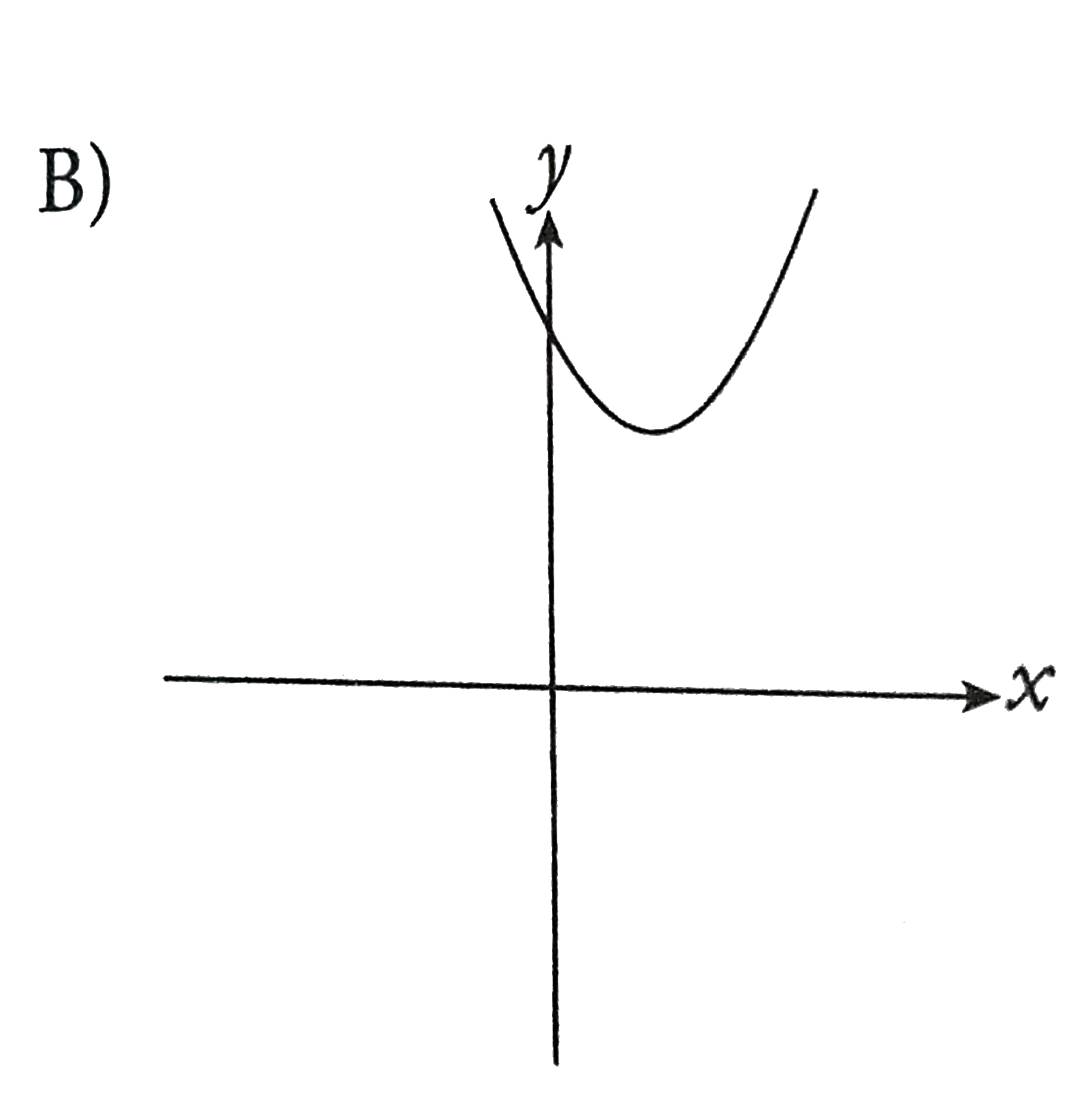 C
C D
D
Given the graph of f(x), draw the graph each one of the following functions :
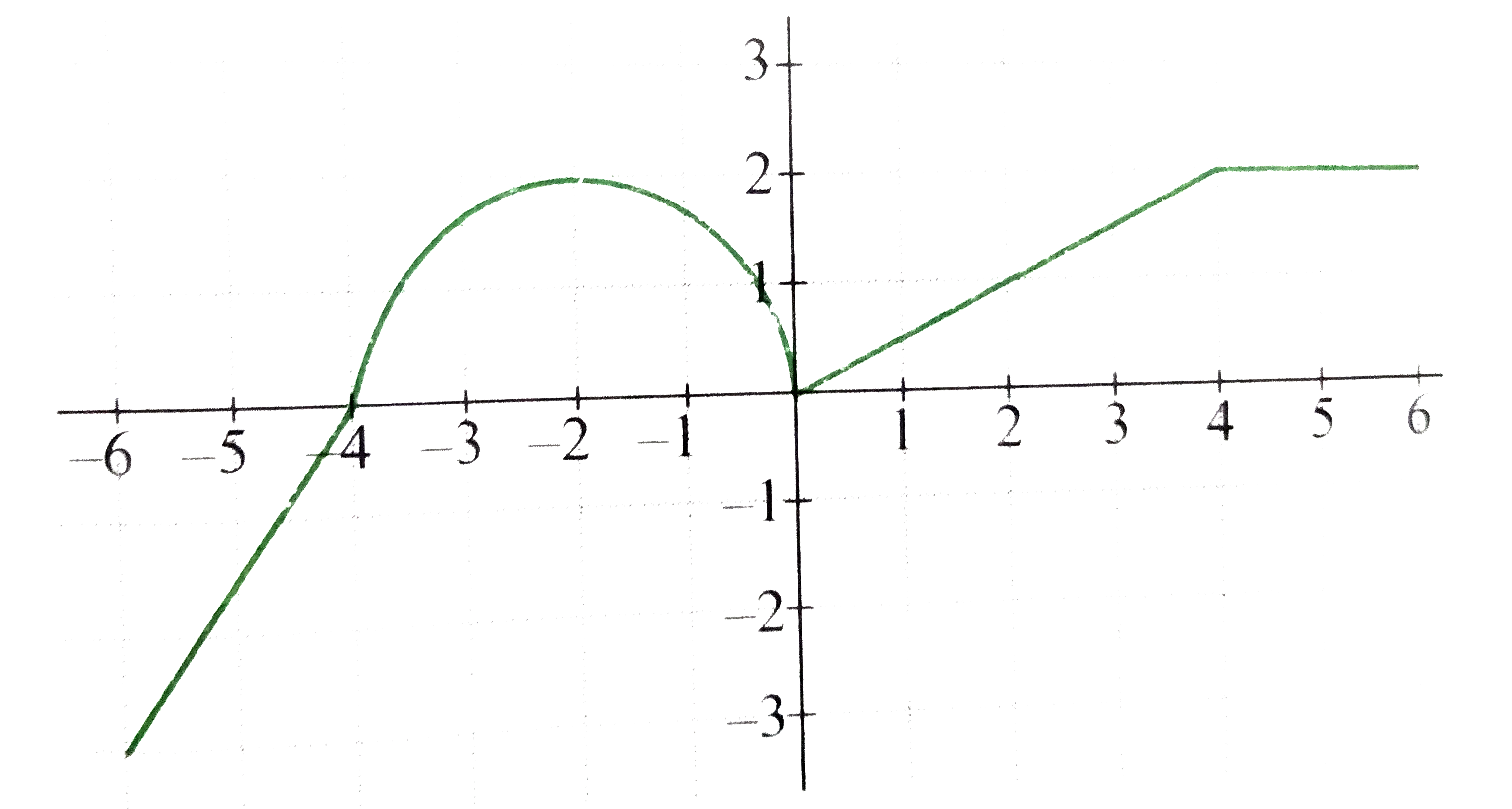
(a) y=f(x)+3 (b) y=−f(x)+2
(c ) y=f(x+1)−2 (d) y=−f(x−1)
(e ) y=f(−x) (f) y=f(|x|)
(g) y=f(1−x)
View SolutionWhich one of the following function(s) is/are homogeneous? (a)f(x,y)=x−yx2+y2 (b) f(x,y)=x13y−23tan−1(xy) (c) f(x,y)=x(ln√x2+y2−lny)+yexy (d) none of these
View SolutionIf the graph of the function y=f(x) is as shown :

the graph of y=12(|f(x)|−f(x)) is
View SolutionGiven the graph of y=f(x).
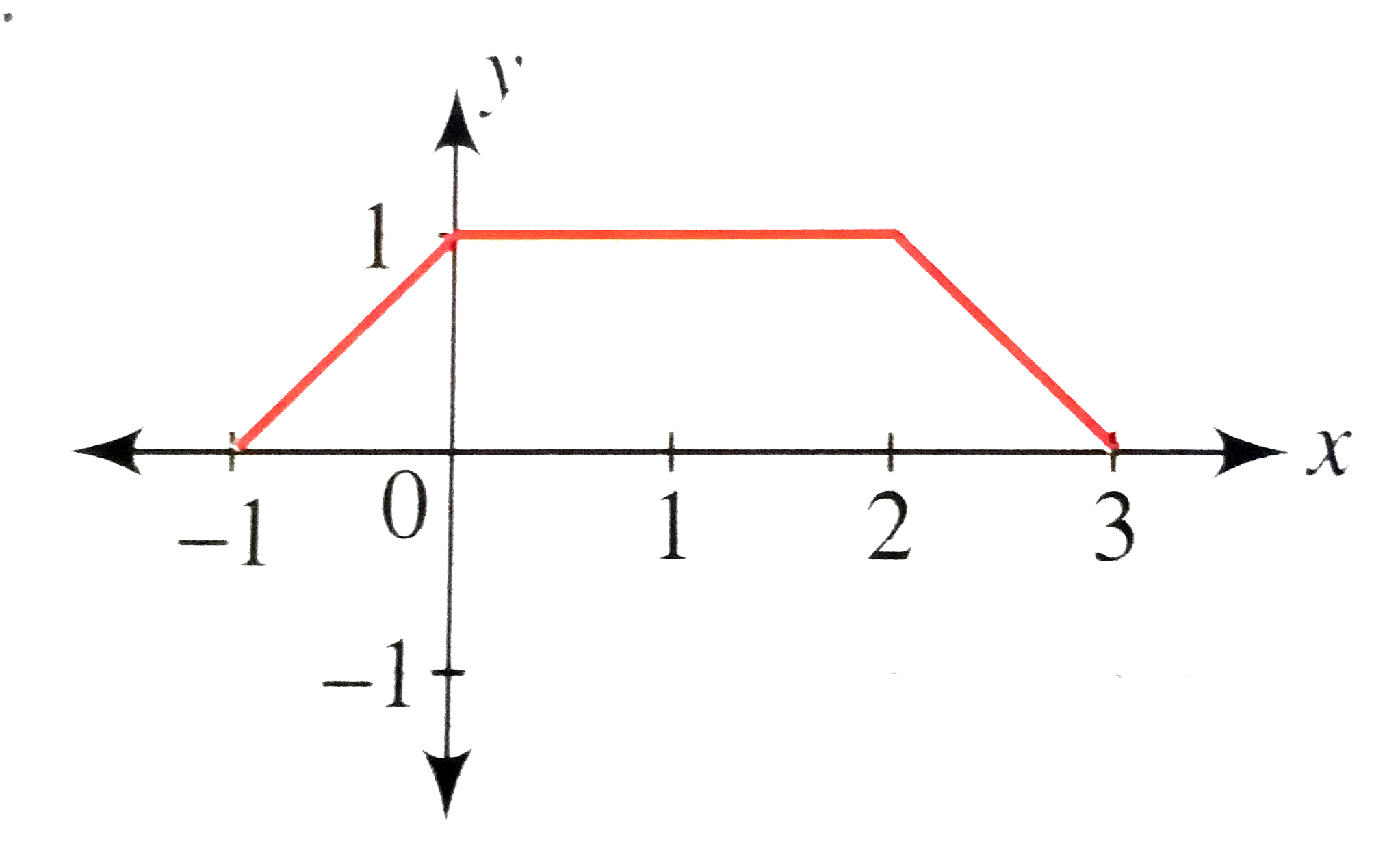
Draw the graphs of the followin.
(a) y=f(1−x) (b) y=−2f(x)
(c) y=f(2x) (d) y=1−f(x)
View SolutionLet f(x) be a function such that f(x).f(y)=f(x+y), f(0)=1,f(1)=4. If 2g(x)=f(x).(1−g(x))
View SolutionIf the graph of the function y=f(x) is as shown :

The graph of y=1/2(|f(x)|−f(x)) is
View SolutionIf the graph of the function y=f(x) is as shown :

The graph of y=1/2(|f(x)|−f(x)) is
View Solution