Express the HCF of 468 and 222 as where are integers in two different ways.
To express the HCF of 468 and 222 in the form of 468x+222y, we will follow these steps:
Step 1: Find the HCF of 468 and 222 using the Division Method
1. Divide 468 by 222:
468÷222=2(quotient)
468−(222×2)=468−444=24(remainder)
2. Now, divide 222 by the remainder 24:
222÷24=9(quotient)
222−(24×9)=222−216=6(remainder)
3. Next, divide 24 by the remainder 6:
24÷6=4(quotient)
24−(6×4)=24−24=0(remainder)
Since the remainder is now 0, the HCF is the last non-zero remainder, which is 6.
Step 2: Express the HCF (6) in the form 468x+222y
We will use the steps of the division process to express 6 as a linear combination of 468 and 222.
1. From the second division step:
6=222−9×24
2. Substituting for 24 from the first division step:
24=468−2×222
Substituting this into the equation for 6:
6=222−9×(468−2×222)
6=222−9×468+18×222
6=(1+18)×222−9×468
6=19×222−9×468
Thus, we can express 6 as:
6=−9×468+19×222
Step 3: Another way to express the HCF
We can also express the HCF in a different way by rearranging the terms.
1. From the first equation:
6=222−9×(468−2×222)
Rearranging gives:
6=19×222−9×468
Thus, we can express 6 as:
6=−9×468+19×222
Final Result
We have expressed the HCF of 468 and 222 in two different ways:
1. 6=−9×468+19×222
2. 6=19×222−9×468
1. Divide 468 by 222:
468÷222=2(quotient)
468−(222×2)=468−444=24(remainder)
222÷24=9(quotient)
222−(24×9)=222−216=6(remainder)
24÷6=4(quotient)
24−(6×4)=24−24=0(remainder)
We will use the steps of the division process to express 6 as a linear combination of 468 and 222.
6=222−9×24
24=468−2×222
Substituting this into the equation for 6:
6=222−9×(468−2×222)
6=222−9×468+18×222
6=(1+18)×222−9×468
6=19×222−9×468
6=−9×468+19×222
We can also express the HCF in a different way by rearranging the terms.
6=222−9×(468−2×222)
Rearranging gives:
6=19×222−9×468
6=−9×468+19×222
We have expressed the HCF of 468 and 222 in two different ways:
1. 6=−9×468+19×222
2. 6=19×222−9×468
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
Given the set of data 1,1,2,2,2,3,3,x,y, where x and y represent two different integers. If the mode is 2, which of the following statements must be true?
AIf x=1 or 3, then y must=2BBoth x and y must be gt 3CEither x or Y must =2DIt does not matter what values x and y have - Question 2 - Select One
Which could be the graph of y=x2+3x+k , where k is an integer ?
A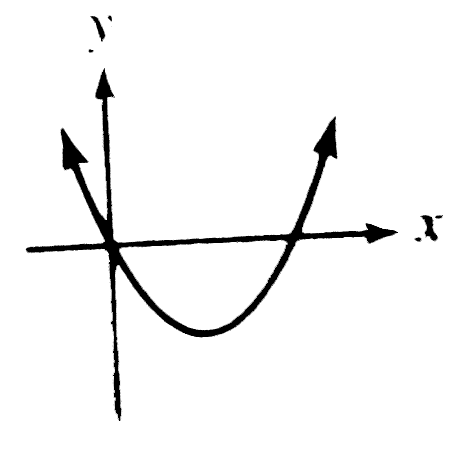 B
B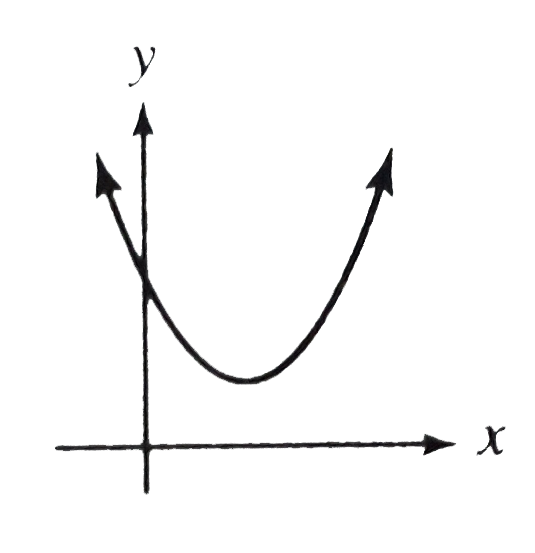 C
C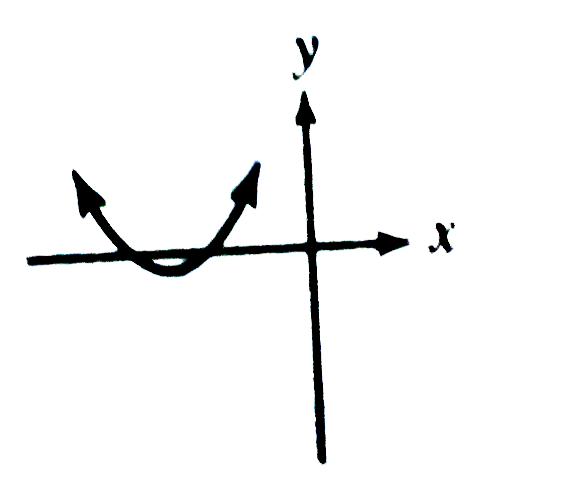 D
D
The number of positive integers with the property that they cann be expressed as the sum of the cubes of 2 positive integers in two different ways is
View SolutionExpress {(x,y):x2+y2=25 where x,y∈W} as a set of ordered pairs.
View SolutionExpress each of the following as a fractions in the form xy where x, y , ∈1andy≠0,
2.−476View SolutionDraw the graph of [y]=sinx,x∈[0,2π] where [⋅] denotes the greatest integer function
View SolutionExpress {(x,y):x2+y2=25,wherex,y∈W} as a set of ordered pairs.
View SolutionCheck whether the following statement is true or not: p: If x,y are integers such that xy is even then at least one of x and y is an even integer.
View Solution

