Fig. 12.3 depicts an archery target marked with its five scoring areas from the center outwards as Gold, Red, Blue, Black and White. The diameter of the region representing Gold score is 21 cm and each of the other bands is 10.5 cm wide. Find the area of each of the five scoring regions.

Radius (r1) of the gold region = 212 cm = 10.5 cm
Given that each circle is 10.5 cm wider than the previous circle.
Therefore, radius (r2) of the 2nd circle = 10.5 cm + 10.5 cm = 21 cm
Radius (r3) of the 3rd circle = 21 cm + 10.5 cm = 31.5cm
Radius (r4) of the 4th circle = 31.5cm+10.5cm=42 cm
Radius (r5) of the 5th circle = 42cm+10.5cm=52.5cm
Area of the gold region = Area of the 1st circle = pir₁^2 = pi (10.5)^2 = 346.5 cm^2
Area of the red region = Area of the 2nd circle - Area of the 1st circle
= πr22−πr21
= π(21)2−π(10.5)2cm2
= (1386−346.5)cm2
= 1039.5cm2
Area of blue region = Area of 3rdcircle - Area of 2ndcircle
= πr23−πr22
= π(31.5)2−π(21)2cm2
= 992.25π−441πcm2
= 551.25πcm2
= 1732.5cm2
Area of black region = Area of 4thcircle - Area of 3rd circle.
= πr24−pr23
= π(42)2−π(31.5)2
= 1764π−992.25π
= 771.75π
= 2425.5cm²
Area of white region = Area of 5thcircle - Area of 4 thcircle
=πr25−πr24
= π(52.5)2−π(42)2
= 2756.25π−1764π
= 992.25π
= 3118.5cm²
Hence, areas of the gold, red, blue, black, and white regions are 346.5cm2,1039.5cm2,1732.5cm2,2425.5cm2and3118.5cm2 respectively.
Topper's Solved these Questions
- BOOK - NCERTCHAPTER - AREAS RELATED TO CIRCLESEXERCISE - SOLVED EXAMPLES6videos
AREAS RELATED TO CIRCLES
- BOOK - NCERTCHAPTER - AREAS RELATED TO CIRCLESEXERCISE - EXERCISE 12.316videos
AREAS RELATED TO CIRCLES
- BOOK - NCERTCHAPTER - ARITHMETIC PROGRESSIONSEXERCISE - Exercise 5.320videos
ARITHMETIC PROGRESSIONS
Similar Questions
Fig. 15.6, depicts an archery target marked with its five scoring areas from the centre outwards as Gold, Red, Blue Black and white. The diameter of the region representing Gold score is 21 cm and each of the other bands is 10.5 cm wide. Find the area of each of the five scoring regions.
View SolutionFig. 12.3 depicts an archery target marked with its five scoring areas from the center outwards as Gold, Red, Blue, Black and White. The diameter of the region representing Gold score is 21 cm and each of the other bands is 10.5 cm wide. Find the area of each of the five scoring regions.
 View Solution
View Solutionfigure shows an archery target marked with its five regions of colours outwards as gold,red,blue,black and white.The diameter of the region representing gold score is 42 cm,and each of other band is 21 cm wide.Find the area of each of the five scoring regions.
View SolutionA wooden article was made by scooping out a hemisphere from each end of a solid cylinder, as shown in fig. If the height of the cylinder is 10 cm and its base is of radius 3.5 cm. Find the total surface area of the article.
 View Solution
View SolutionA wooden article was made by scooping out a hemisphere from each end of a solid cylinder, as shown in the figure. If the height of the cylinder is 10 cm and its base of radius 3.5 cm. Find the total surface area of the article.
 View Solution
View SolutionAn archery target has three regions formed by three concentric circles in Fig. 12.73. If the diameters of the concentric circles are in the ratio 1:3:5. then find the ratio of the areas of three regions.
 View Solution
View SolutionIn figure , AB and CD are two diameters of a circle ( with centre O) perpendicular to each other and OD is the diameter of the smaller circle . If OA = 7 cm , find the area of the shaded region.
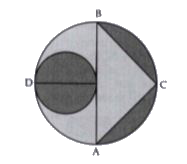 View Solution
View SolutionA wooden article was made by scooping out a hemisphere from each end of a solid cylinder, as shown in Fig. 16.37. If the height of the cylinder is 10 cm, and its base is of radius 3.5 cm, find the total surface area of the article.
View SolutionIn fig. O is the center of a circle such that diameter AB=13cm and AC= 12 cm. BC is joined. Find the area of the shaded region.
View SolutionIn Fig. 12.27, AB and CD are two diameters of a circle (with centre O) perpendicular to each other and OD is the diameter of the smaller circle. If OA=7 cm, find the area of the shaded region
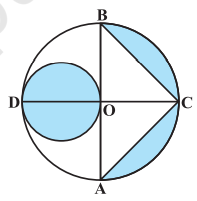 View Solution
View Solution

