Find each of the following products: 736 x 93
To find the product of 736 and 93, we can use the distributive property. Here’s a step-by-step solution:
Step 1: Rewrite the multiplication using the distributive property
We can express \(93\) as \(100 - 7\). Thus, we can rewrite the multiplication as:
\(
736 \times 93 = 736 \times (100 - 7)
\)
Step 2: Apply the distributive property
Now, we can distribute \(736\) to both \(100\) and \(-7\):
\(
736 \times 93 = 736 \times 100 - 736 \times 7
\)
Step 3: Calculate \(736 \times 100\)
Calculating \(736 \times 100\) is straightforward:
\(
736 \times 100 = 73600
\)
Step 4: Calculate \(736 \times 7\)
Now, we will calculate \(736 \times 7\):
- \(7 \times 6 = 42\) (write down \(2\) and carry over \(4\))
- \(7 \times 3 = 21\), plus the carry \(4\) gives \(25\) (write down \(5\) and carry over \(2\))
- \(7 \times 7 = 49\), plus the carry \(2\) gives \(51\)
So, \(736 \times 7 = 5152\).
Step 5: Subtract the two results
Now we need to subtract \(7360\) from \(73600\):
\(
73600 - 5152
\)
Aligning the numbers for subtraction:
73600−5152
Starting from the right:
- \(0 - 2 = 8\) (borrow \(1\))
- \(0 - 5 = 5\) (after borrowing)
- \(6 - 1 = 5\)
- \(3 - 5 = 8\) (borrow \(1\))
- \(7 - 0 = 7\)
So, \(73600 - 5152 = 68448\).
Final Answer
Thus, the product of \(736\) and \(93\) is:
\(
\boxed{68448}
\)
We can express \(93\) as \(100 - 7\). Thus, we can rewrite the multiplication as:
\(
736 \times 93 = 736 \times (100 - 7)
\)
Now, we can distribute \(736\) to both \(100\) and \(-7\):
\(
736 \times 93 = 736 \times 100 - 736 \times 7
\)
Calculating \(736 \times 100\) is straightforward:
\(
736 \times 100 = 73600
\)
Now, we will calculate \(736 \times 7\):
- \(7 \times 6 = 42\) (write down \(2\) and carry over \(4\))
- \(7 \times 3 = 21\), plus the carry \(4\) gives \(25\) (write down \(5\) and carry over \(2\))
- \(7 \times 7 = 49\), plus the carry \(2\) gives \(51\)
Now we need to subtract \(7360\) from \(73600\):
\(
73600 - 5152
\)
73600−5152
Starting from the right:
- \(0 - 2 = 8\) (borrow \(1\))
- \(0 - 5 = 5\) (after borrowing)
- \(6 - 1 = 5\)
- \(3 - 5 = 8\) (borrow \(1\))
- \(7 - 0 = 7\)
Thus, the product of \(736\) and \(93\) is:
\(
\boxed{68448}
\)
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
Find the product of the following reaction
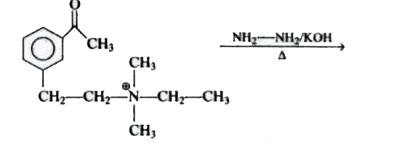 A
A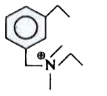 B
B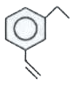 C
C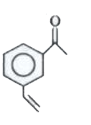 DNone of these
DNone of these - Question 2 - Select One
Find the product of the following reaction:
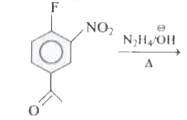 A
A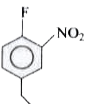 B
B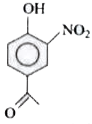 C
C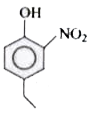 D
D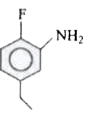
- Question 3 - Select One
Find the product of the following reaction
 A
A B
B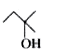 C
C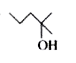 D
D
Find each of the following products: (i) 3×(−8)×5 (ii) 9×(−3)×(−6)
View SolutionFind each of the following products:
(a)5x2×4x3
(b) −3a2× 4b4View SolutionFind each of the following products: (−127a2b2)× (92a3b2c2) (−7xy)×(14x2yz)
View SolutionFind the 'x' in each of the following
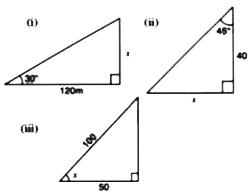 View Solution
View SolutionDetermine each of the following products by suitable rearrangements: 2 x 1497 x 50
View Solution

