Find limx→0f(x) where
f(x)={x|x|x≠00x=0
To find the limit limx→0f(x) where
f(x)={x|x|if x≠00if x=0
we will analyze the function for values approaching 0 from both the left and the right.
Step 1: Analyze the function for x<0
When x<0, the absolute value |x| is equal to −x. Therefore, we can rewrite f(x) as:
f(x)=x|x|=x−x=−1
Step 2: Analyze the function for x>0
When x>0, the absolute value |x| is equal to x. Thus, we can rewrite f(x) as:
f(x)=x|x|=xx=1
Step 3: Calculate the left-hand limit as x→0
The left-hand limit (LHL) is calculated as follows:
limx→0−f(x)=limx→0−−1=−1
Step 4: Calculate the right-hand limit as x→0
The right-hand limit (RHL) is calculated as follows:
limx→0+f(x)=limx→0+1=1
Step 5: Compare the left-hand and right-hand limits
Now we compare the two limits:
- Left-hand limit: LHL=−1
- Right-hand limit: RHL=1
Since LHL≠RHL, we conclude that the limit does not exist.
Final Conclusion
Thus, we have:
limx→0f(x) does not exist.
---
- Right-hand limit: RHL=1
Topper's Solved these Questions
- LIMITS AND DERIVATIVESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - LIMITS AND DERIVATIVESEXERCISE - EX -13.2
11 Videos
- LIMITS AND DERIVATIVESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - LIMITS AND DERIVATIVESEXERCISE - Miscellaneous Exercise
30 Videos
- LIMITS AND DERIVATIVESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - LIMITS AND DERIVATIVESEXERCISE - EX-13H
10 Videos
- INTRODUCTION OF THREE DIMENSIONAL GEOMETRYBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - INTRODUCTION OF THREE DIMENSIONAL GEOMETRYEXERCISE - Miscellaneous Exercise
6 Videos
- LINEAR INEQUALITIESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - LINEAR INEQUALITIESEXERCISE - MISCELLANEOUS EXERCISE
14 Videos
Similar Questions
limx→0xsecx
View SolutionEvaluate limx→0f(x), where
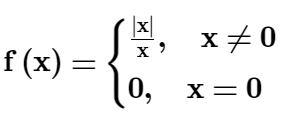
View SolutionFind limX→0f(x) where f(x)={xx≠05x=0}
View SolutionFind limx→0f(x), where f(x)=⎧⎪⎨⎪⎩x−1x<00x=0x=1x>0
View SolutionFind limx→1f(x), where f(x)={x+1x≠10x=1}
View Solutionf(x)={x2x2+|x|x≠01x=0then f(x) is
View Solutionlimx→0(x3logx)
View Solutionlimx→0sinxx=?
View SolutionLet f(x) be a function defined by f(x)={3x|x|+2xx≠00x=0
Show that limx→0f(x) does not exist.
View SolutionEvaluate (lim)x→0f(x), where f(x)={|x|x, x≠0,0, x=0
View Solution
